Um elétron está confinado no estado fundamental de um
poço finito com
(a) Qual é o maior comprimento de onda de luz capaz de
libertar o elétron do poço de potencial por absorção de um
único fóton?
(b) O elétron, que se encontra inicialmente no estado fun-
damental, pode absorver luz com um comprimento de
onda Se a resposta for afirmativa, qual é a
energia do elétron após a absorção?
Passo 1
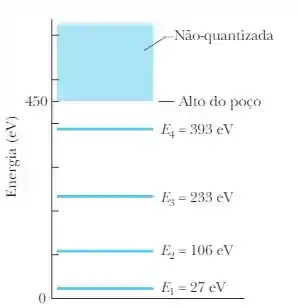
a) Primeiro precisamos saber qual é a energia que liberta o elétron do poço, assim pegamos o estado em que se encontra o elétron e fazemos a diferença entre o potencial do posso e a energia do estado, dessa forma:
Para o elétron ser libertado por absorção de um único fóton, o fóton deve ter no minímo essa energia, assim:
E
Então:
Isolando o , temos:
Substituindo os valores e , temos:
Passo 2
b) Agora para o comprimento de onda de , temos que avaliar se a energia é suficiente para libertar o elétron.
Como o comprimento de onda anterior era maior e a energia libertava o elétron, o comprimento de onda dado também o fará e ainda forncerá ao elétron energia cinética. Pois o comprimento de onda é inversamente proporcional a energia, como na equação:
Vamos então calcular a energia excedente:
A energia miníma necessária para libertar o elétron é , o restante é convertido em energia cinética. Dessa forma, a energia cinética do elétron libertado é: