Um elétron no estado do poço de potencial finito da Fig.39-7 absorve uma energia de de uma fonte externa.
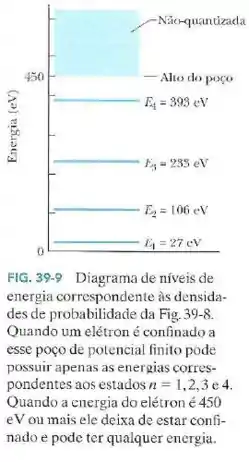
Use o diagrama de níveis de energia da Fig.39-9 para determinar a energia cinética do elétron após essa absorção, supondo que o elétron é transferido para uma posição na qual .
Passo 1
Pelo diagrama de níveis de energia, como o elétron está inicialmente no estado , ele possui uma energia .
Após absorver energia de uma fonte externa, sua energia final fica:
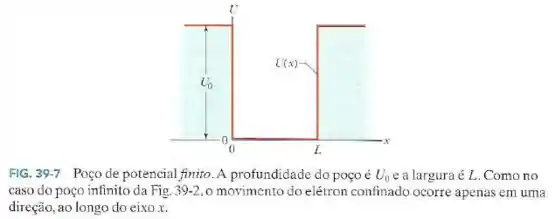
Assim, ele passa a ser uma partícula livre do poço de potencial. Ele sendo transferido para a região onde a energia potencial (de acordo com o diagrama de níveis energéticos), a sua energia cinética será:
Resposta
Exercícios de Livros Relacionados
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 5 do potencial finito do poço quadrado
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 4 do potencial finito do poço quadrado
Como sugere a figura 39-8, a densidade de probabilidade na região 0xL do poço de potencial finito da figura 39-7 varia senoidalmente, de acordo com a equação ψ 2 x = B s e n 2 k x , onde B é uma const
Como sugere a figura 39-8, a densidade de probabilidade na região xL do poço de potencial finito da figura 39-7 diminui exponencialmente, de acordo com a equação ψ 2 x = C e - 2 k x , onde C é uma con