Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Partícula no Poço Finito

Ver Teoria
Exercício 7123456891011121314

Enunciado

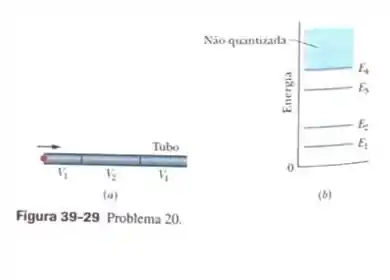
A Fig. 39-29a mostra um tubo fino no qual foi montado um poço de potencial finito, com

V 2 = 0 V . Um elétron se move para a direita no interior do poço, em uma região onde a tensão é V 1 = - 9,00 V , com uma energia cinética de 2,00 e V . Quando o elétron penetra no poço, pode ficar confinado se perder energia suficiente, emitindo um fóton. Os níveis de energia no interior do poço são E 1 = 1,0 e V ,   E 2 = 2,0 e V   e E 3 = 4,0 e V e a região quantizada começa em E 4 = 9,0 e V , como mostra o diagrama de níveis de energia da Fig. 39-29b. Qual é a menor energia (em e V ) que o fóton pode assumir?

Passo 1

Como o elétron está penetrando no poço, a energia que ele tem está na região não quantizada, então a menor energia que o fóton pode ter com a emissão do elétron é do nivel E 4 para o E 3 para que ele fique confinado. A diferença desses níveis é:

E 4 - E 3 = 9,0 e V - 4,0 e V = 5,0 e V

Passo 2

Além dessa energia, o fóton também vai possuir toda a energia cinética do elétron, porque é necessário que ele também perca essa energia para cair do poço. Então:

E f ó t o n = E + K =   5,0 e V + 2,0 e V = 7,0 e V

Resposta

E f ó t o n = 7,0 e V

Exercícios de Livros Relacionados

Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 5 do potencial finito do poço quadrado
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 4 do potencial finito do poço quadrado
Como sugere a figura 39-8, a densidade de probabilidade na região 0xL do poço de potencial finito da figura 39-7 varia senoidalmente, de acordo com a equação ψ 2 x = B s e n 2 k x , onde B é uma const
Como sugere a figura 39-8, a densidade de probabilidade na região xL do poço de potencial finito da figura 39-7 diminui exponencialmente, de acordo com a equação ψ 2 x = C e - 2 k x , onde C é uma con