Para o circuito inteiro abaixo, calcule:
O fator de potência. a potência média liberada pela fonte. a potência reativa. a potência aparente. a potência complexa.
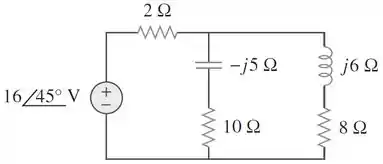
Passo 1
Vamos começar pela letra . O primeiro passo é encontrar a impedância equivalente do circuito. Já que o seu ângulo será o ângulo do fator de potência. A impedância equivalente desse circuito será:
Portanto, o fator de potência será:
Lembrando que o fator de potência é atrasado porque o seu ângulo é positivo.
Passo 2
Na letra temos que encontrar a potência média liberada pela fonte. Potência média é o mesmo que potência ativa e potência real, ou seja, é .
Agora para achar a potência média nós precisamos descobrir a potência total e ela será:
Com isso a potência total (ou aparente):
A fonte de está em RMS.
Passo 3
Para encontrar a potência reativa e aparente é só lembrar do triângulo das potências.
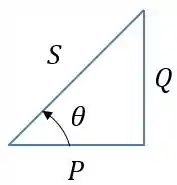
Com isso a potência reativa será:
Passo 4
Como , a potência aparente será:
Com isso a potência total (ou aparente), como foi efetuado o calculo no passo 2, temos
Passo 5
Como foi estudado na teoria, a potência complexa pode ser escrita nesta forma:
Logo, substituindo as potências calculadas nos passos acimas: