Para o sistema de potência da figura abaixo, determine:
- A potência média
- A potência reativa
- O fator de potência
Note que é um valor RMS.
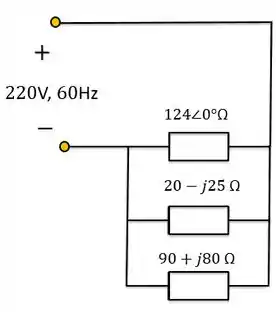
Passo 1
Para calcular a potência média, precisamos lembrar da fórmula:
Já foi fornecido o valor da tensão. Precisamos, então, calcular o valor da corrente que passa no circuito e o ângulo do fator de potência.
Passo 2
Para calcular a corrente que passa pelo circuito, vamos utilizar a Lei de Ohm:
No caso do circuito acima, como todas as impedâncias estão em paralelo, a tensão será:
Passo 3
Para calcular a corrente, falta ainda calcularmos a impedância equivalente do circuito. Como elas estão em paralelo:
Passo 4
Para finalizar o cálculo da impedância equivalente total, temos que fazer o cálculo do paralelo de com a impedância .
Lembrando que o ângulo do fator de potência é o ângulo da impedância, que, neste caso, será o da impedância total:
Passo 5
Finalmente, a corrente será:
Passo 6
Para calcular a potência média, colocamos os dados calculados na fórmula:
Passo 7
Por fim, precisamos calcular a potência reativa:
Se a gente analisar, o sinal da potência reativa deu negativo. Isso significa que a carga é predominantemente capacitiva.