Determine a potência complexa liberada por para o circuito da figura. Seja .
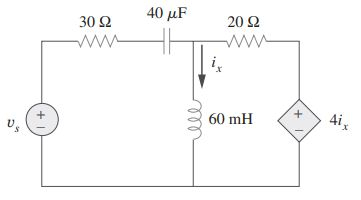
Passo 1
Vamos começar separando os dados:
Agora vamos calcular as impedâncias no domínio da frequência:
Para o indutor:
(lembrando que tudo tem que estar no Sistema Internacional)
Para o capacitor:
Passo 2
Agora vamos redesenhar o circuito com os valores encontrados no passo 1
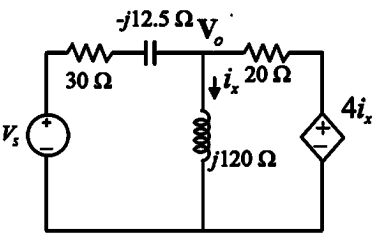
Passo 3
Vamos então aplicar a Lei das Correntes de Kirchhoff ao único nó do circuito (vamos chamar sua tensão de ) para encontrar o a partir da Lei de Ohm, veja:
Mas… quem é ?
Pela Lei de Ohm, , então, substituindo isso na equação anterior…
Passo 4
Agora, a corrente da fonte será:
Passo 5
Podemos então, calcular nossa potência complexa:
Resposta
Exercícios de Livros Relacionados
40- Elabore um problema para ajudar outros estudantes a entender melhor a potência aparente e o fator de potência.
57- Para o circuito da Figura 11.76 , determine as potências média, reativa e complexa pela fonte de corrente dependente.
85- Um sistema residencial comum de um circuito trifilar monofásico permite a operação de eletrodomésticos de 120V , bem como de 240V , ambos a 60H z . O circuito residencial tem como modelo aquele mo
Determine a expressão de regime permanente para as correntes i g e i L no circuito da Figura P10.55, quando vg = 400 cos 400t V.Determine o coeficiente de acoplamento. c) Determine a energia armazenad
As três cargas do circuito da Figura P10.30 podem ser descritas da seguinte forma: a carga 1 é um resistor de 240Ω em série com uma reatância indutiva de 70Ω ; a carga 2 é uma reatância capacitiva de