Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potência Complexa

Ver Teoria
Exercício 12345678910

Enunciado

Obtenha o fator de potência para cada um dos circuitos abaixo. Especifique se cada fator de potência está adiantado ou atrasado.

Passo 1

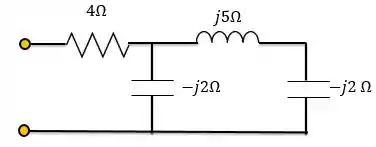
O fator de potência é o cosseno do ângulo da impedância equivalente do circuito. Logo, para o primeiro circuito, teremos que:

Z e q = { j 5 - j 2 ( - j 2 ) } + 4

Z e q = { j 3 ( - j 2 ) } + 4

Z e q = j 3 × - j 2 j 3 - j 2 + 4

Z e q = 6 ∠ 0 ° j 1 + 4

Z e q = 6 ∠ 0 ° 1 ∠ 90 ° + 4

Z e q = 6 ∠ - 90 ° + 4

Z e q = 4 - j 6

Z e q = 7,21 ∠ - 56,31 °   Ω

Passo 2

O fator e potência para o primeiro circuito, será, então:

cos ⁡ - 56,31 ° = 0,554

Como o ângulo da impedância equivalente deu um número negativo, o fator de potência está adiantado. Ou seja: a carga é predominantemente capacitiva.

Passo 3

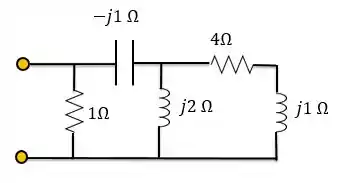
Para o próximo circuito, vamos fazer os cálculos em etapas:

Z e q 1 = ( 4 + j 1 ) ( j 2 )

Z e q 1 = 4 + j 1 × j 2 4 + j 1 + j 2

Z e q 1 = 4,12 ∠ 14,04 ° × 2 ∠ 90 ° 4 + j 1 + j 2

Z e q 1 = 8,25 ∠ 104,04 ° 4 + j 3

Z e q 1 = 8,25 ∠ 104,04 ° 5 ∠ 36,87 °

Z e q 1 = 1,65 ∠ 67,17 °   Ω

Passo 4

Agora temos que calcular a impedância equivalente para a outra parte do circuito:

Z e q 2 = ( Z e q 1 ) + ( - j 1 )

Z e q 2 = ( 1,65 ∠ 67,17 ° ) + ( - j 1 )

Z e q 2 = 0,634 + j 1,52 - j 1

Z e q 2 = 0,634 + j 0,52

Z e q 2 = 0,82 ∠ 39,36 °   Ω

Passo 5

Finalmente:

Z e q T o t a l = ( Z e q 2 ) ( 1 )  

Z e q T o t a l = 0,82 ∠ 39,36 ° × 1 0,634 + j 0,52 + 1  

Z e q T o t a l = 0,82 ∠ 39,36 ° 1,634 + j 0,52

Z e q T o t a l = 0,82 ∠ 39,36 ° 1,71 ∠ 17,65 °

Z e q T o t a l = 0,478 ∠ 21,7 °   Ω

Passo 6

O fator e potência para o segundo circuito, será, então:

cos ⁡ 21,7 ° = 0,93

Como o ângulo da impedância equivalente deu um número positivo, o fator de potência está atrasado. Ou seja: a carga é predominantemente indutiva.

Resposta

Primeiro circuito: FP = 0,554 adiantado

Segundo circuito: FP = 0,93 atrasado

Exercícios de Livros Relacionados

40- Elabore um problema para ajudar outros estudantes a entender melhor a potência aparente e o fator de potência.
57- Para o circuito da Figura 11.76 , determine as potências média, reativa e complexa pela fonte de corrente dependente.
85- Um sistema residencial comum de um circuito trifilar monofásico permite a operação de eletrodomésticos de 120V , bem como de 240V , ambos a 60H z . O circuito residencial tem como modelo aquele mo
Determine a expressão de regime permanente para as correntes i g e i L no circuito da Figura P10.55, quando vg = 400 cos 400t V.Determine o coeficiente de acoplamento. c) Determine a energia armazenad
As três cargas do circuito da Figura P10.30 podem ser descritas da seguinte forma: a carga 1 é um resistor de 240Ω em série com uma reatância indutiva de 70Ω ; a carga 2 é uma reatância capacitiva de