O macaco hidráulico da Figura abaixo está cheio com óleo a . Desprezando o peso dos dois pistões, qual a força que é necessária na alavanca para suportar o peso de indicado no desenho?
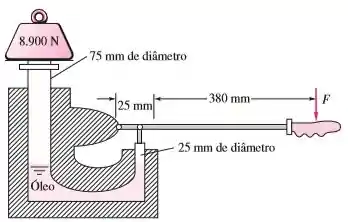
Passo 1
Essa é uma questão de transmissão de força, de multiplicar a força usando um sistema hidráulico.
Isso nos remete a Pascal e como vimos na teoria:
A força no lado é e a área desse pistão é
E a área do lado é de
Assim, conseguimos descobrir a força necessária que seja aplicada no pistão para suportar o peso em .
Passo 2
Agora que descobrimos o valor da força que deve ser aplicada no pistão , conseguimos através de equilíbrio de momento descobri qual o valor da força na alavanca irá gerar essa força .
Fazendo equilíbrio de momento temos:
O ponto analisado será o inicio da alavanca. Senso assim a força está a desse ponto e a força está .
A equação de momento será:
O referencia de sinal adotado foi girar no sentido horário negativo, por isso e girar no sentido anti-horário positivo.
Agora podemos descobrir o valor de .