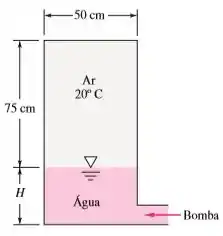
O tanque cilíndrico na Figura abaixo está sendo cheio com água a por uma bomba que desenvolve uma pressão de saída de . No instante mostrado, a pressão no ar é de e . A bomba para quando ela não pode mais aumentar a pressão da água. Para compressão isotérmica do ar, calcule H naquele instante.
Passo 1
A bomba vai parar de encher o tanque de água quando a pressão no tanque for igual a pressão que ela exerce. Assim:
Nesse momento teríamos uma coluna de água . E de ar igual a , pois a altura do tanque é de .
Então teríamos a seguinte equação:
Para resolvermos o problema precisamos encontrar o valor da pressão final de ar. O que é fácil se lembrarmos de termodinâmica. Da fórmula “PiViTi-PoVoTo”. Como é uma compressão isotérmica, temos:
Então para encontrarmos o valor de , precisamos encontrar a forma com que a pressão de ar irá variar de acordo com o valor de .
Passo 2
Então se tivermos a pressão no início, o volume no início, e o volume no final, descobrimos a pressão no final por uma regra de três.
A pressão no início é dada pelo enunciado
Agora vamos calcular o volume inicial. O volume de um cilindro é área da base vezes altura.
Chamando a área da base de , temos que o volume ocupado por no início era de:
E o volume final será em função de , sendo assim:
Passo 3
Agora temos tudo para descobrir a pressão final
Agora sim, temos tudo em função de .
Passo 4
Tendo tudo em função de , podemos substituir na equação de pressão no final:
Agora teremos uma equação do segundo grau assim:
Resolvendo a equação do segundo grau, achamos dois valores
e
Como o tem que ser menor que o único valor possível é