
A) 8
B) 4
C) 2
D) 1
E) 0,5
Passo 1
Escrever a resistência de cada um dos cilindros:
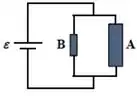
são os comprimentos dos cilindros e respectivamente. e são suas áreas. A resistividade é a mesma para os dois condutores pois o enunciado fala que eles são feitos do mesmo material.
Passo 2
Relacionar os comprimentos e as áreas. Se tem o dobro do diâmetro de , então a área é quatro vezes maior que a área de . Isso porque:
Além disso, o enunciado diz que .
Assim, temos que:
Passo 3
Dividir a resistência de pela resistência de (calculadas no primeiro passo) e substituir as equações do passo :
Passo 4
Calcular a razão entre as potências e substituir o que achamos no passo :
Resposta
Letra (c): .