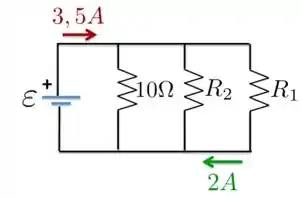
No circuito indicado na Figura abaixo, a taxa de dissipação da energia elétrica de é igual a .
- Determine e .
- Qual é a fem da bateria?
- Ache a corrente que passa por e pelo resistor de .
- Calcule o consumo total de energia elétrica em todos os resistores e a energia elétrica fornecida pela bateria. Mostre que seus resultados estão de acordo com a conservação de energia.
Passo 1
a) Então, vamos lá? Bom, para começar, o enunciado dá o valor da potência dissipada no resistor , que é de , e conhecemos da Figura o valor da corrente que passa nesse resistor,
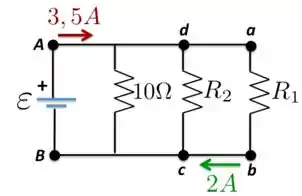
Agora que temos o valor dessa resistência, podemos encontrar o valor do potencial entre os pontos e , que a mesma ddp entre os resistores e , ambos em paralelo com . Portanto
Essa é ddp da resistência equivalente , por onde passa a corrente de mostrada na Figura. Concorda? Checa isso para ver se faz sentido....checou?
A resistência equivalente nesse caso é
Simplificando essa expressão, obtemos que
Essa resistência está submetida à uma ddp de , o que dá pra gente que
Resolvendo essa equação, temos que é
Passo 2
b) A fem da bateria é a mesma a que está a resistência equivalente que, por sua vez, é a mesma que está entre os pontos e . Então,
Passo 3
c) Como o resistor está a uma ddp de , então a corrente que passa por esse resistor é
Pelo resistor de , que também está a uma ddp de , a corrente é
Passo 4
d) A potência total fornecida pela bateria é
A potência dissipada pelo resistor é de . Já no resistor , a potência dissipada é de
No resistor de , a potência é
Se a gente soma todas as três potências dissipadas em cada resistor, teremos exatamente o valor de , que é o valor total da potência fornecida pela bateria. Isso mostra que há conservação de energia