UFRJ- Física 3 – PF 2018.2 - DIURNO – 14
Três resistores idênticos de resistência podem ser combinados de duas formas distintas, como mostrado na figura abaixo. Em ambos os arranjos, a combinação é conectada a uma bateria que fornece uma diferença de potencial constante , como indicado. Sejam e as potências dissipadas pelos resistores em destaque nos arranjos e , respectivamente. Podemos afirmar que a razão vale:
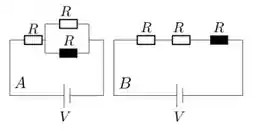
- 1
Passo 1
Para encontrarmos essas potências dissipadas, temos que calcular
Portanto, precisamos encontrar qual é a corrente que passa nos resistores destacados.
No caso do arranjo , temos dois resistores em paralelo cujo resistor equivalente estará em série com outro de . Começando com os dois em paralelo em :
Este em série com , vai resultar em uma resistência equivalente
Em , teremos uma corrente igual a
Agora, como essa corrente vai ser dividida em duas partes iguais, uma vez que os resistores em paralelo em são iguais, a corrente que passa no resistor destacado é
Passo 2
Em , a resistência equivalente é igual , já que todos estão associados em série. Por isso, a corrente que passa em cada um dos resistores é a mesma e igual a
Então, as potências dissipadas em cada um dos resistores destacados nos arranjos e são iguais:
Resposta
Letra g).