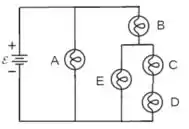
6ª questão - A figura mostra um circuito elétrico constituído de algumas lâmpadas idênticas e uma bateria ideal. Qual das alternativas expressa corretamente o brilho relativo entre as lâmpadas:
A)
B)
C)
D)
E)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Para essa questão, foi dado um circuito elétrico com uma fonte de tensão e várias lâmpadas idênticas dispostas em série e paralelo.
Nosso objetivo aqui é ordenar as lâmpadas da que tem o maior brilho para a que quem o menor brilho.
Tem ideia de como fazer isso? 🤔
Mas talvez podemos pensar “ué, as lâmpadas são idênticas, como o brilho de todas não é igual?” 🤔
Realmente, as lâmpadas são idênticas, mas como as lâmpadas estão conectadas de diversas maneiras no circuito, a tensão fornecida a cada uma nem sempre será igual.
Hã?? Como assim??
Bora lá que eu te explico! 😁
Passo 2
Quando temos uma fonte de tensão significa que entre os terminais positivo/negativo da fonte, a tensão é de (Volts).
Dependendo de como uma carga está ligada a uma fonte, a tensão nos terminais da carga pode ser diferente.
No caso, quando dizemos que todas as lâmpadas são idênticas, na verdade, para nosso problema, estamos dizendo que todas possuem a mesma carga . Com isso, quanto maior a tensão em seus terminais, maior será seu brilho!
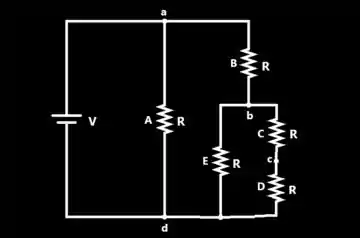
Vamos usar o ponto como o ponto de referência de já que é onde está ligado o polo negativo da nossa fonte.
A lâmpada está conectada entre os terminais e onde também está conectada a fonte de tensão . Lembra que quando dois componentes estão ligados nos mesmos nós, é o mesmo que dizer que eles estão em paralelo? E quando dois componentes estão em paralelo, como é a tensão entre eles? 🤔
Iguais, não é?
Com isso, vemos que possui uma tensão .
Entendeu isso? 👀
Passo 3
Agora perceba que esse conjunto de lâmpadas , , e estão em paralelo com a lâmpada e com a fonte de tensão .
Então temos que descobrir qual é a tensão entre os nós e . Pra isso vamos usar uma formula de divisão de tensão que usamos quando temos duas cargas em série.
Quando temos
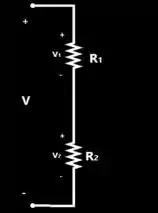
Pode parecer um pouco diferente do nosso caso pois é um único resistor e no nosso caso temos resistores ocupando seu lugar.
Então o que podemos fazer é calcular a resistência equivalente entre os nós e .
Bora lá? 😎
Passo 4
O que queremos é transformar a junção dos resistores , e em um único resistor equivalente
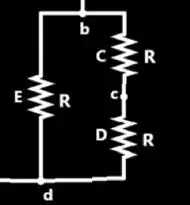
Primeiro, começamos com a associação entre e , perceba que um emenda o outro para chegar em , portanto eles estão em série.
Associação em série de resistores fazemos como? Somando, não é? 😁
Logo
Imaginando e como um único resistor, resultamos em dois resistores em paralelo, correto? Ambos estão ligados nos mesmos nós.
Nesse caso a associação de resistores paralelos é feita como
Substituindo pelos seus valores, temos
Agora podemos calcular a divisão de tensão!
A resistência equivalente entre os nós e é .
Bora lá!
Passo 5
Agora aplicamos o cálculo da divisão de tensão na seguinte configuração
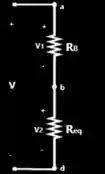
Vamos primeiro calcular a tensão na lâmpada
Fazendo as substituições das resistências
Logo, será
Com isso, vamos que a tensão em é de .
Tranquilo até aqui?
Passo 6
Por fim, vamos fazer o mesmo para para obter a tensão entre os nós e .
Substituindo...
Assim resultando em
Assim a tensão na lâmpada e na associação em série das lâmpadas e é de !
Como a tensão entre e é de , fazendo a divisão de tensão entre e , podemos afirmar que a tensão em cada uma é a metade de . Não confia, veja só!
Como
Viu só? 😎
Passo 7
Agora que temos a tensão em todas as lâmpadas, vamos recapitular.
A tensão na lâmpada é igual a tensão na fonte, ou seja, .
A tensão na lâmpada foi calculada como .
A tensão na lâmpada é a mesma tensão da lâmpada que é igual a ou
E a tensão na lâmpada foi calculada como .
Como a tensão na lâmpada está relacionada diretamente com sua luminosidade, então organizando as lâmpadas em ordem decrescente de tensão, temos
Analisando as alternativas, vemos que a letra D) é a alternativa que condiz com nossos resultados!
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
D)