Considere a malha de resistores da figura abaixo.
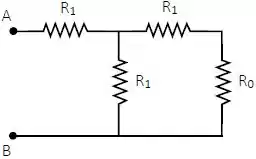
Para que a resistência equivalente entre os terminais e seja , o resistor deve ter o valor:
;
;
;
;
;
;
Passo 1
Um bom caminho é simplificar o circuito aos poucos, vamos começar com as resistências em série e .
Passo 2
Agora temos em paralelo as resistências e . Assim:
Substituindo a expressão que encontramos no Passo 1:
Passo 3
Por último, temos em série as resistências e . Logo:
Substituindo a expressão que encontramos no Passo 2, teremos:
Passo 4
No entanto, queremos que essa resistência equivalente seja igual a , logo:
Agora é arrumar a bagunça, vamos lá!
Finalmente:
Resposta
;
Exercícios de Livros Relacionados
71- Um resistor R 1 consome uma energia elétrica P 1 , quando conectada a uma f e mϵ . Quando o resistor R 2 é conectado a mesma f e m , ela consome energia elétrica P 2 . Em termos de P 1 e P 2 , qua
Uma combinação em paralelo dos resistores A e B está conectada aos terminais de uma bateria. O resistor A tem o dobro da resistência do resistor B . Se a corrente conduzida pelo resistor A é I , então
Na Fig. 27-82, uma fonte ideal de força eletromotriz ε =12,0V é ligada a um circuito cujasresistências s ã oR 1=6,00Ω ,R 2=12,00Ω ,R 3=4,00Ω ,R 4=3,00ΩeR 5=5,00Ω ã . Qual é a diferença de potencial da
Uma lâmpada de120V com dois filamentos pode operar em três níveis de potência: 100 ,200 e300W . Um dos filamentos queima. Depois disso, a lâmpada funciona com a mesma luminosidade (dissipa a mesma pot
Um equipamento possui um resistor X que se projeta de uma abertura lateral. Esse resistor é conectado a outros três resistores, como indica a Figura 26.38. Um ohmímetro conectado através de a e b regi