Um resistor cilíndrico de comprimento deveria ter uma seção reta ao longo de todo seu comprimento e uma resistência igual a . Devido a um erro de fabricação, metade do resistor apresenta uma seção reta , conforme a figura.
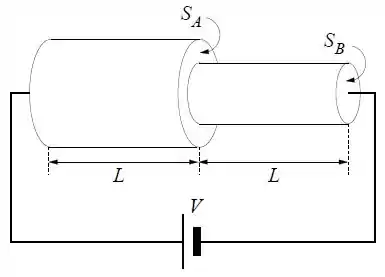
Determine a resistência do resistor em termos do valor projetado .
Aplica-se uma ddp de volts nas extremidades do resistor. Calcule os módulos dos campos elétricos e em cada um dos trechos do resistor em termos de e .
Passo 1
Determine a resistência do resistor em termos do valor projetado .
Bom, se esse cara fosse construído da mesma forma que foi planejado, com área transversal e comprimento , a sua resistência seria dada por:
Beleza! Mas alguém fez merda e o resistor saiu com essa cara...
Vamos pensar o seguinte... se vem uma corrente da esquerda para a direita, ela vai passar primeiro pela parte do resistor com área transversal e depois pela parte do resistor com área transversal , concorda?
Então seria a mesma coisa dizer que esses dois caras estão em série, conseguiu enxergar isso?
Assim, a resistência será:
O problema já nos disse que . Então voltando ao problema:
Nós já achamos ali em cima que:
E como temos que comparar com , vamos tentar dar uma arrumada no pra poder substituir o :
Passo 2
Aplica-se uma ddp de volts nas extremidades do resistor. Calcule os módulos dos campos elétricos e em cada um dos trechos do resistor em termos de e .
Quando aplicamos a ddp nas extremidades do resistor, deve ser igual à soma das ddps de cada uma das duas partes do resistor.
Além disso, podemos associar a ddp com o campo elétrico através da relação , logo:
Agora que já encontramos a relação entre , e , precisamos descobrir uma relação entre e .
Como esses dois caras estão em série, a corrente que passa pelas duas partes deve ser a mesma , assim, através da Lei de Ohm:
Novamente vamos usar a relação que o problema nos deu, :
Agora ficou fácil! Vamos substituir isso na expressão de para encontrarmos e em função de e .
Passo 3
Começando por:
Teremos:
Beleza! Para encontrar temos apenas que fazer a substituição inversa:
Portanto:
Resposta