Considere o circuito indicado na Figura abaixo. A corrente que passa pelo resistor de é igual a no sentido indicado. Quais são as correntes que passam pelos resistores de e ?
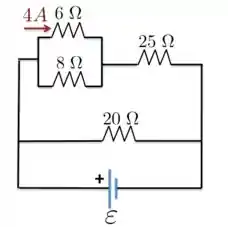
Passo 1
Para começar o exercício, dá uma olhada na Figura abaixo, e repara que a gente tem, além da corrente dada no enunciado de , as correntes e . Para começar, as correntes de e se somam no ponto para dar a corrente , isto é,
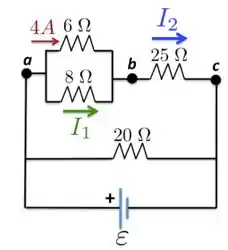
Agora, entre os pontos e , temos dois resistores em paralelo. Isso significa, como já vimos na teoria, que esses resistores estão à mesma diferença de potencial . No resistor de , a ddp é de
Portanto, como essa é também a ddp para o resistor de , então
Disso, temos que a corrente que passa no resistor de é
Passo 2
Então, para completar nossa solução do exercício, repara lá na Figura que o resistor de está à mesma diferença de potencial que tem os resistores entre os pontos e , então:
Para a gente saber que ddp é essa, podemos encontrar a resistência equivalente entre os pontos e por onde passa a corrente total . Então, os resistores de e estão em paralelo e o resultado disso está em série com o de , concorda?
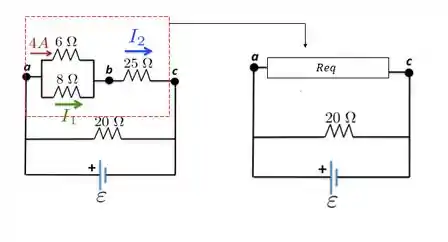
Bom, colocando isso em contas, temos
Portanto, a ddp entre as extremidades do resistor de é
Então, a corrente que passa pelo resistor de é
Resposta
No resistor de passa uma corrente de
e no de , uma de