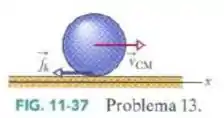
Um jogador de boliche arremessa uma bola de raio ao longo de uma pista. A bola (Fig. 11-37) desliza sobre a pista com velocidade inicial e a velocidade angular inicial . O coeficiente de atrito cinético entre a bola e a pista é . A força de atrito cinético , que age sobre a bola produz uma aceleração linear e uma aceleração angular. Quando a velocidade diminui o suficiente e a velocidade angular aumenta o suficiente, a bola pára de deslizar e passa a rolar suavemente. (a) Qual é o valor de em termos de nesse instante? Durante o deslizamento, quais são (b) a aceleração linear e (c) a aceleração angular da bola? (d) Por quanto tempo a bola desliza? (e) Que distância a bola desliza? (f) Qual é a velocidade linear da bola quando começa a rolar suavemente?
Passo 1
Como dito no enunciado, o movimento da bola é dividido em duas partes:
- Deslizamento: A força de atrito age diminuindo a velocidade linear e aumentando a velocidade angular, até esta última chegar no valor certo para a bola começar a rolar;
- Rolamento: A força de atrito cinético deixa de agir e a bola entra em um movimento regular de translação e rotação.
Se a velocidade linear e a velocidade angular estão mudando, temos aceleração linear e aceleração angular agindo! Vamos fazer o diagrama de corpo livre da bola pra tentar entender:
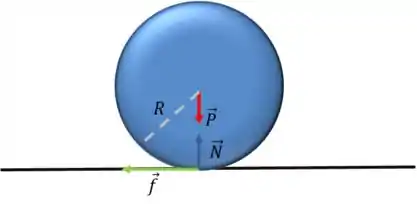
Agora vamos analisar como essas forças agem em cada movimento: rotação e translação.
Passo 2
Na translação, temos que a bola não se move na vertical, portanto, pela primeira lei de Newton:
Vamos arbitrar que o eixo cresce para a direita, no mesmo sentido da velocidade inicial da bola. Portanto, usando a segunda lei de Newton no eixo horizontal:
é a força de atrito cinético, portanto, tem valor constante:
E então:
Substituindo os valores:
Isso responde a letra (b), mas vamos guardar o nosso resultado!
Passo 3
Já para a rotação, temos que, em relação ao centro de massa da esfera, somente a força realiza torque, portanto:
Sabemos que tem valor constante:
Se usarmos a segunda lei de Newton da rotação:
O momento de inércia da esfera é tabelado:
Portanto:
E conseguimos o valor para a aceleração angular:
Substituindo os valores:
Isso responde a letra (c)!
Passo 4
Aprendemos que a característica principal do rolamento sem deslizamento é:
Substituindo os valores:
Isso nos responde a letra (a)!
Passo 5
Agora nós temos a relação entre e , bem como essas duas grandezas variam com o tempo, saca só:
Juntando tudo, temos:
Dessa equação, já temos os valores de:
- , dado no enunciado, é igual a
- , encontrado no Passo 2, é igual a
- , dado no enunciado, é igual a
- , encontrado no Passo 3, é igual a
Substituindo os valores:
Show! Estamos quase lá! Isso aí já responde a letra (d).
Passo 6
Com o tempo que a bola fica deslizando, é fácil encontrar as respostas das letras (e) e (f).
Pra descobrirmos a distância, vamos usar a equação clássica da cinemática:
Com:
- Queremos descobrir quanto ela andou, portanto,
- , dado no enunciado, é igual a
- , encontrado no Passo 2, é igual a
- , encontrado no Passo 5, é igual a
Substituindo tudo:
Respondendo, assim, a letra (e).
Passo 7
É agora hein! Pra terminar! Só usar mais uma equação clássica da cinemática:
Onde:
- , dado no enunciado, é igual a
- , encontrado no Passo 2, é igual a
- , encontrado no Passo 5, é igual a
Substituindo:
Fechou! Respondemos o que faltava.