UFMG; Fundamentos de mecânica; Provas – P1; 2022.1; Questão P1.2
Na figura ao lado vê-se uma montagem. A bolinha de massa é lançada para cima por uma rampa que faz um ângulo com a horizontal, saindo da rampa a uma altura a partir do solo. Mede-se que a bolinha leva um tempo para atingir o solo, a partir do instante que sai da rampa.
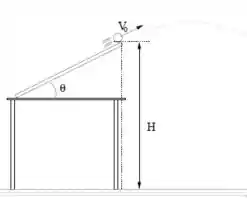
P1.2 – calcule a distância horizontal que a bolinha percorrerá do instante que ela saiu da rampa até o momento que se choca com o solo.
Passo 1
Faaaala galera! Tudo certinho com vocês?? Bora lá resolver mais um probleminha!
Se liga que essa gente vai resolver juntos e bem rápido, segue comigo então.
Dado o tipo de movimento realizado pela bolinha ao sair da rampa como a aceleração da bolinha na horizontal é nula, ela ficou com velocidade horizontal constante até cair no chão.
Ela gastou o tempo para atingir o chão e, durante esse intervalo de tempo, ficou com a velocidade Como observado na imagem abaixo:
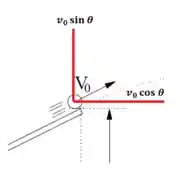
Dessa maneira, a equação da distância horizontal é dada por:
Passo 2
Para calcular podemos usar justamente o tempo de queda, , dado.
Sabemos que durante o movimento de queda, a bolinha executa um movimento retilíneo uniformemente variado no eixo , o eixo vertical. Assim, podemos escrever:
Como é dado por:
E, a aceleração é justamente , vem:
Mas, é o tempo que a bolinha leva para chegar ao solo. Logo:
Assim:
Isolando , temos:
Passo 3
Agora podemos voltar à equação da distância. Substituindo o resultado de nessa equação temos:
E tá aí nossa resposta, curtiu?? Te vejo na próxima.