Uma pedra esférica, uniforme e maciça parte do repouso e rola pra baixo de uma colina de de altura. A metade superior da colina é áspera o suficiente para fazer a pedra rolar sem deslizar, mas a metade inferior está coberta de gelo e não há atrito. Dado: momento de inércia de uma esfera girando ao redor do eixo que passa pelo seu centro de massa:
- Desenhe as forças que agem sobre a pedra quando ela desce a parte superior da colina, justificando o sentido da força de atrito.
- Qual é o modulo da velocidade de translação da pedra quando ela atinge a base da colina?
- Qual é o módulo da velocidade angular da pedra na base da colina?
Passo 1
a):
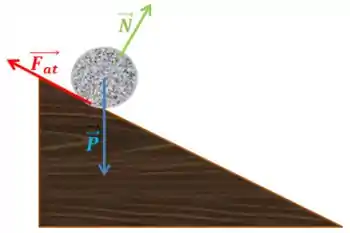
Onde:
Normal.
Peso.
: Força de atrito.
A força de atrito tem esse sentido porque deve fazer a esfera girar no sentido horário, já que ela está descendo o plano.
Passo 2
b):
Bom galera, aqui a gente tem que usar a conservação de energia entre a altura máxima da colina e a metade da sua altura, já que ali é o ultimo ponto onde há força de atrito capaz de fazer a bola girar.
Assim:
Só que a energia cinética é a soma da energia cinética de translação mais de rotação:
Além de que:
Beleza? Então:
Vamos usar ali a condição de rolamento que diz que:
Então:
Beleza. Essa é a velocidade na metade superior da colina. Agora precisamos calcular a velocidade na metade inferior. Pra isso, é só usar a conservação da energia mecânica:
Passo 3
c):
Após a força de atrito, a rotação não muda, já que não há mais uma força aplicando o torque na bola. Assim, podemos calcular a velocidade de rotação final usando a velocidade:
E:
Então:
Resposta
a):
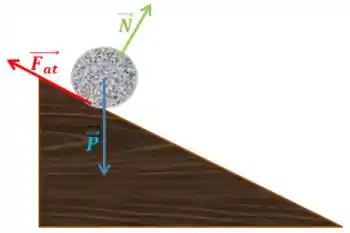
b):
c):