Seja um cilindro maciço e homogêneo, de raio e massa ,(cilindro 1) que pode girar sem atrito em torno de um eixo vertical que passa pelo seu centro. O eixo está fixado em uma mesa horizontal, sobre a qual se encontra o cilindro. Enrolada na superfície curva do cilindro há uma corda inextensível, que passa por uma roldana e tem na extremidade livre um outro cilindro (cilindro 2) de massa que cai sob a ação da gravidade. As massas da roldana e da corda são desprezíveis e a corda não desliza.
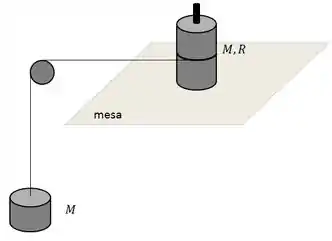
Seja agora a situação em que não há um eixo no interior do cilindro que esteja fixo à mesa, de
modo que o cilindro 1 está livre para deslizar, sem atrito, sobre a mesa. Permanecem as
condições anteriores sobre a corda, a roldana e o cilindro que cai. Nesta nova situação,
b) Escreva as equações de movimento do cilindro 1 e do cilindro 2 (isto é, escreva as equações que relacionam as forças existentes com as acelerações) .
c) Obtenha a relação entre a aceleração do cilindro 2 e as acelerações do cilindro 1.
d) Calcule a tensão na corda.
Passo 1
b)
Vamos lá. De agora em diante temos uma nova situação:
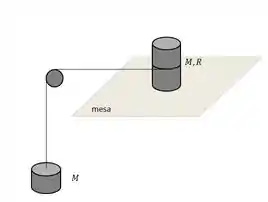
Agora, além de rotacionar, o cilindro 1 também transalada, porque não tem mais o eixo segurando ele. O cilindro 2 vai cair por ação da gravidade. Mas agora, temos uma mudança importante: O vínculo não pode mais ser usado, porque o cilindro está deslizando.
Então as acelerações dos cilindros vão ser diferentes.
Então vamos escrever as equações de movimento para os dois cilindros:
Primeiro, para o cilindro 1:
Olhando o cilindro 1 de cima:
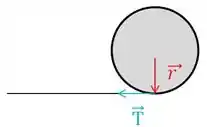
Então:
Usando a relação entre torque e aceleração angular:
Beleza, essa é a equação para rotação do cilindro 1.
Agora vamos ver a de translação, ainda para o cilindro 1:
A única força que puxa ele pra esquerda é a tração, como não temos movimento na vertical, o peso e a normal se anulam. Então:
Beleza, essa é a equação para tranlação do cilindro 1.
Para o cilindro 2, que só desce, continua a mesma coisa da letra a:
Suave?
Passo 2
(c)
A aceleração total do cilindro 1 é:
Que a aceleração de translação somada a aceleração tangencial da borda do cilindro.
Como quem tá causando essa aceleração total é a aceleração do cilindro 2, que ta puxando o cilindro 1, temos que a relação entre as acelerações é:
Sucesso??
Passo 3
(d)
Agora ele quer a tensão. Então é só uma brincadeira com as equações que conhecemos:
Usando a equação de movimento para o cilindro 2 que achamos na letra b:
Usando a relação entre as acelerações que achamos na letra c:
Agora, usando a equação de movimento de rotação do cilindro 1, que achamos na letra b:
Isolando o e substituindo o momento de inércia :
Agora, usando a equação de movimento de translação do cilindro 1, que achamos na letra b
Isolando o
Maravilha!! Agora voltando, e substituindo as acelerações:
Ajeitando:
Então:
Show! Isso é tudo pessoal!!
Resposta
(b) Para o cilindro 1
Rotação:
Translação:
Para o cilindro 2
Translação:
(c)
(d)