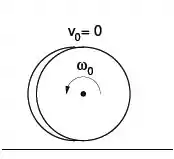
Um disco sólido uniforme é posto em rotação com velocidade angular em torno de um eixo horizontal, perpendicular ao plano do disco, passando por seu centro de massa. Depois, a borda do disco é posta em contato com uma superfície horizontal, e o disco é solto, com
seu eixo de rotação paralelo à superfície, como na figura ao lado. Seja o raio do disco, sua massa e seu momento de inércia em torno do centro de massa, e seja o coeficiente de atrito cinético entre o disco e a superfície. Em termos de ,, e da aceleração da gravidade :
a)Qual é o tempo necessário para que o disco deixe de derrapar?
b)Qual é a velocidade angular do disco no momento em que ele deixa de derrapar?
c)Qual é a distância percorrida enquanto o disco está derrapando?
d) Calcule a razão entre a energia cinética final e a energia cinética inicial do disco.
Passo 1
a)
Vamos antes de tudo isolar as forças que agem no corpo?

Escrevendo a Segunda Lei de Newton para rotação, a gente vai ter:
O torque também pode ser calculado por . Nesse caso, o Peso e a Normal estão com a linha de atuação passando no eixo de rotação, logo a única força que causará torque é a força de atrito. Assim, teremos:
Passo 2
Mas ah, enquanto o disco derrapa temos o que podemos chamar de rolamento com deslizamento mas quando ele para de derrapar e começa só a rolar vamos ter apenas o rolamento. Uma das características do rolamento é que a velocidade do centro de massa pode ser calculada por:
Na iminência de começar a rolar, o atrito entre o disco e o chão é cinético, que pode ser calculado por:
Substituindo na fórmula do , teremos:
Para achar a aceleração, pela Segunda Lei de Newton oficial, teremos:
Passo 3
Das equações da cinemática a gente pode relacionar o com e o com e daí utilizar a relação que sabemos que temos que usar em algum momento, pois é a condição do problema:
Já para a velocidade linear:
Como vamos ter:
Passo 4
Fazendo , vai restar...
Passo 5
b)
Já vimos ali em cima a relação que podemos utilizar pra resolver essa letra b, é ela:
Tacando o que a gente já sabe a questão sai!
Passo 6
c)
Para achar a distância percorrida nesse tempo basta calcular a integral da velocidade, que é o deslocamento. Assim, podemos escrever:
Passo 7
d)
No início só temos rotação, logo a única energia cinética será de rotação e a expressão é simplesinha.
Já falei pra vocês que quando o disco começar a deslizar haverá o que chamamos de rolamento sem deslizamento e . Haverá energia cinética de translação e rotação, podendo ser achadas por:
Como calculamos no Passo 5, .
Substituindo no , a gente vai ter:
Dividindo um pelo outro, vai restar: