Calcular o diâmetro de um tirante que sustente, com segurança, a carga descrita no esquema abaixo. O material do tirante tem limite de escoamento a tração de .
Vamos utilizar como coeficiente de segurança.
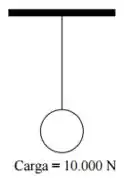
Passo 1
O tirante está sendo tracionado por uma carga :
Nosso objetivo nesse exercício é calcular o diâmetro do tirante para que essa carga não gere uma tensão normal média maior que a tensão normal admissível :
Essa é a nossa condição de projeto.
Se calcularmos os valores de (em função do diâmetro do tirante) e de e substituirmos esses valores nessa expressão, poderemos isolar o diâmetro e descobrir o seu valor.
Para calcular a tensão normal média e a tensão normal admissível , vamos usar as suas fórmulas:
Do enunciado do exercício, sabemos que:
- O material do tirante falha por escoamento (se deforma irreversivelmente) quando a tensão normal no tirante atinge a tensão normal de falha ;
- E que deve ser usando um fator de segurança nesse projeto: .
Passo 2
Vamos começar calculando a tensão normal média :
Como o tirante está sob tração pura, a força normal interna vai ser igual à intensidade dessa tração.
Por outro lado, a área da seção transversal do tirante é calculada em função de seu diâmetro através da fórmula da área do círculo .
Substituindo esses valores na equação da tensão normal média, temos:
Como :
Passo 3
Agora, vamos calcular a tensão normal admissível :
Substituindo os valores e :
Passo 4
Aplicando a condição de projeto:
Substituindo os valores encontrados:
Queremos encontrar , então devemos isolá-lo:
Espelhando a expressão (para deixar ela mais fácil de visualizar) e fazendo a raiz quadrada dos dois lados:
Calculando a expressão à direita, isso dá: