Um cordão flexível de comprimento total , sendo a distância horizontal entre os suportes, é amarrado nos suportes e situados em elevações diferentes. Uma carga está pendurada em uma pequena roldana que rola ao longo do cordão, sem atrito, até chegar à posição de equilíbrio em .
Sabendo que a carga de ruptura do cordão é e se deseja um coeficiente de segurança , calcular a carga admissível .
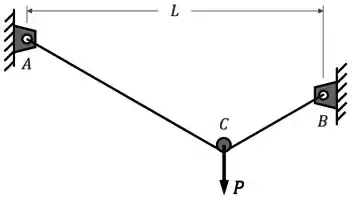
Passo 1
O que está acontecendo com a roldana?
Se a gente se lembrar de quando estudamos polias e roldanas lá em física, vamos nos lembrar que quando um cordão é tracionado, a força de tração é igual em todos os pontos do cordão.
Isso significa que a força no ponto está sendo equilibrada por duas forças de tração iguais:
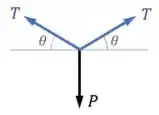
A gente pode afirmar que os ângulos dessas duas forças são iguais, como está desenhado na figura, porque isso é necessário para que as componentes horizontais das duas forças se cancelem.
E com o cordão?
Bom, o exercício disse que o cordão rompe quando a tração nele atinge a carga de ruptura .
Mas não é a carga máxima permitida no cordão.
Na realidade, como se deseja um coeficiente/fator de segurança , a carga máxima permitida no cordão, que vamos chamar de tração admissível , vai ser dada por:
E o que é que o exercício quer?
O exercício quer saber a carga admissível , que vai ser a carga na roldana que gera no cordão a tração máxima permitida .
A gente consegue relacionar com usando o equilíbrio de forças, mas, para fazer isso, vamos precisar saber o valor de para podermos calcular o valor da componente vertical das trações.
Para encontrar esse , vamos ter que usar um pouco de geometria e as informações de que:
- é a distância entre os suportes;
- E é o comprimento total do cordão.
Passo 2
Vamos começar tentando descobrir o valor de , já que esse é provavelmente o maior desafio do exercício.
Bom... O ângulo que as forças de tração fazem com a horizontal é o próprio ângulo que o cordão faz com a horizontal.
Então podemos adicionar esses ângulos ao desenho do enunciado:
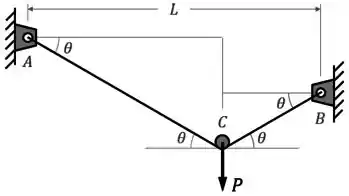
Agora, vamos chamar a distância entre e de “”, a distância entre e de “”, o comprimento do cordão entre e de “” e o comprimento do cordão entre e de “”:
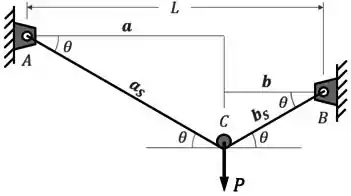
Com isso, podemos perceber que:
Mas se também percebermos que e que , isso fica:
Mas é o próprio comprimento total do cordão:
E como o enunciado disse que :
Isolando o cosseno, temos que:
Calculando, isso dá:
E, por fim, usando que , encontramos que:
Passo 3
Com encontrado, agora podemos partir para relacionar a carga com a tração .
Mais especificamente, queremos relacionar a carga admissível (que é o que queremos encontrar) com a tração admissível (que vimos no primeiro passo que é igual a ).
Para fazer isso, fazemos um diagrama de corpo livre do ponto :
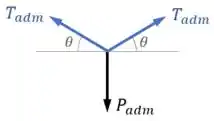
E, em seguida, aplicamos o equilíbrio de forças.
Como nos interessa encontrar , que está na vertical, fazemos o equilíbrio de forças na vertical:
Na vertical, temos apontando para baixo e as componentes verticais das duas trações , que são calculadas multiplicando pelo seno de , apontando para cima.
Então o nosso equilíbrio de forças fica assim:
Isolando :
Substituindo e :
Calculando , chegamos ao resultado: