A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for . Use um fator de segurança para cisalhamento .

Passo 1
O que está acontecendo?
Cada parafuso precisa transmitir metade da força total de .
Como eles estão sob cisalhamento duplo, então a força cortante interna neles vai ser igual a metade da força que eles precisam transmitir.
Isso significa que, no final das contas, a força cortante interna em cada parafuso é da força total de :
Fazer um desenho da análise de esforços internos nesses parafusos não é muito comum, mas se for preciso, pode ser feito assim:
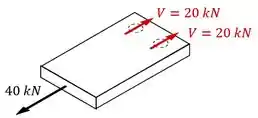
Essa força cortante é responsável por gerar uma tensão cisalhante média nos parafusos.
O que é que o exercício quer?
O exercício quer saber qual o diâmetro dos parafusos para que essa força cortante em cada um deles não gere uma tensão cisalhante média acima de uma certa tensão admissível:
Sendo que essa tensão admissível é obtida dividindo a tensão de falha (nesse caso, a tensão de ruptura por cisalhamento ) pelo fator de segurança .
Podemos calcular dessa forma, e calcular em função do diâmetro dos parafusos.
Ao substituir esses valores na condição de projeto , vamos poder isolar o diâmetro e encontrar o seu valor mínimo.
Passo 2
Vamos começar definindo as tensões cisalhante média e cisalhante admissível.
A tensão cisalhante média em um parafuso é dada pela sua fórmula:
Podemos expressar a área da seção transversal de um parafuso como a área de um círculo em função de seu diâmetro: . Assim temos:
Já a tensão cisalhante admissível vai ser dada pela fórmula:
Passo 3
Aplicando a condição de projeto:
Substituindo as expressões encontradas:
Queremos encontrar , então devemos isolá-lo:
Espelhando essa expressão (para deixar ela mais fácil de visualizar) e fazendo a raiz quadrada dos dois lados:
Substituindo os valores , e :
Como , podemos reescrever a força de como para que o resultado final saia mais facilmente em :
Calculando a expressão da direita, isso dá:
Assim, o diâmetro exigido é: