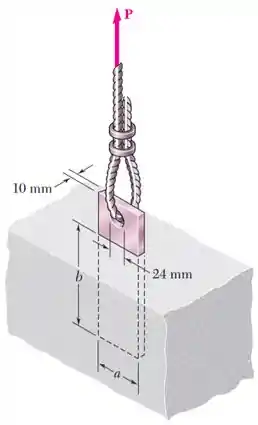
Uma chapa de de espessura está encaixada em um bloco de concreto e é utilizada para ancorar um cabo vertical de alta resistência, conforme mostra a figura. O diâmetro do furo na chapa é de , o limite de resistência do aço utilizado é e o limite da tensão de aderência entre a chapa e o concreto é .
Sabendo que se deseja um coeficiente de segurança de quando , determine () a largura necessária para a chapa e () a dimensão mínima com que a placa deve ser encaixada no bloco de concreto. (Despreze a tensão normal entre o concreto e a extremidade inferior da placa.)
Passo 1
O que está acontecendo?
Esse conjunto pode falhar, fazendo o bloco de concreto se soltar, de duas formas:
1. A tensão normal média na chapa de aço pode superar o limite .
Sobre essa tensão normal média na chapa, podemos observar duas coisas:
- Ela é causada basicamente pela tração realizada pela força , de tal forma que a força normal interna na chapa é igual à ;
- E ela é maior na seção transversal da chapa que é mais reduzida pelo furo de diâmetro , já que essa seção vai possuir a menor área para resistir à força normal .

2. Ou o conjunto pode falhar se a tensão cisalhante média entre as superfícies da chapa e do concreto superar o limite .
Quanto a essa tensão cisalhante média , podemos observar:
- Que ela é distribuída ao longo da área das laterais da chapa submersas no bloco de concreto;
- Que dessas laterais tem dimensões e tem dimensões , em que é a espessura de da chapa;
- E que, para manter o equilíbrio da chapa de aço, essa tensão tem que corresponder a uma força cortante resultante igual à força :
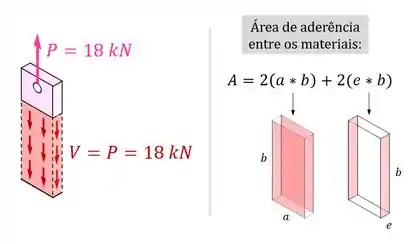
E o que é que o exercício quer?
Ele quer saber quais são as dimensões mínimas e para que sejam satisfeitas as condições de projeto:
Sendo que as tensões admissíveis e não são as tensões de falha e , mas sim essas tensões divididas pelo fator de segurança :
Passo 2
Vamos começar calculando as tensões admissíveis para a tensão normal na chapa e para a tensão cisalhante de aderência entre a chapa e o concreto:
Substituindo , e :
Calculando, isso dá:
Passo 3
Tensões admissíveis calculadas, agora podemos aplicar as condições de projeto .
Começando pela tensão normal na chapa de aço:
Usando a fórmula da tensão normal média :
Bom, nos interessa avaliar a seção crítica da chapa: a seção onde a tensão normal média é maior.
Como vimos anteriormente, essa seção crítica é a seção mais ocupada pelo furo de diâmetro , que é a menor seção transversal em toda a chapa:
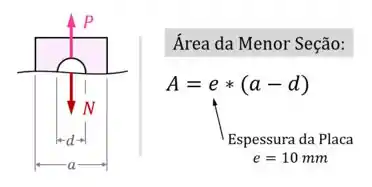
Como para o equilíbrio interno da chapa, a força normal interna deve ser igual a e como nessa seção crítica, a área é de , a equação anterior fica assim:
Queremos descobrir o valor necessário para a dimensão , então devemos isolar ela.
Passando a parte que está dividindo para o outro lado, temos:
Dividindo tudo por :
Terminando de isolar :
Do enunciado, temos que , e .
Além disso, encontramos que .
Substituindo esses valores, temos:
Calculando, isso dá:
Encontrado o valor necessário para a dimensão !
Passo 4
Para encontrar o valor necessário para a dimensão , vamos partir para a próxima condição de projeto, referente a tensão cisalhante de aderência entre os materiais:
Usando a fórmula da tensão cisalhante média :
Como vimos, as superfícies onde essa aderência age são as laterais da chapa submersas no concreto:
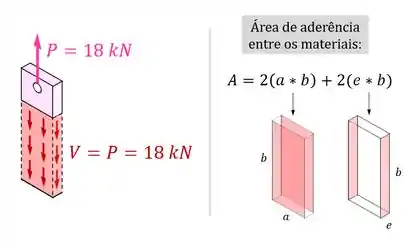
Substituindo a força cortante e a área de aderência , nossa equação anterior fica assim:
Queremos encontrar o valor necessário para a dimensão , então precisamos isolá-la.
Deixando em evidência:
Multiplicando os dois lados por :
Espelhando a equação e dividindo os dois lados por :
Do enunciado, temos que e .
Além disso, encontramos que e que .
Substituindo esses valores, temos:
Calculando, isso dá:
Ou seja, esse é o valor mínimo necessário para a dimensão .
Resposta
(a) ;
(b) .