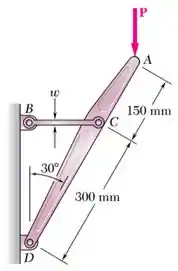
O vínculo horizontal tem de espessura, uma largura e é feito de um aço que tem um limite de resistência à tração de . Qual é o coeficiente de segurança, se a estrutura mostrada for projetada para suportar uma carga ?
Passo 1
O que está acontencdo?
A força gera um momento na peça que tenta fazer a peça girar em volta do ponto .
Esse momento é equilibrado por um momento oposto gerado pela força que o vínculo faz na peça :
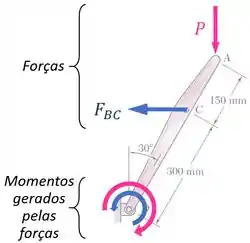
Como reação à essa força, a peça faz no vínculo uma força oposta de mesma intensidade .
O apoio em equilibra essa força, e o vínculo fica, no final das contas, sob uma tração de intensidade :
![]()
Essa tração gera no vínculo uma força interna normal que, por sua vez, gera nele uma tensão normal média .
O que precisamos fazer?
O exercício quer saber qual é o coeficiente/fator de segurança no vínculo.
O fator de segurança é a razão entre a tensão de falha e a tensão normal média , ou seja:
A tensão de falha nesse caso corresponde ao limite de resistência a tração de .
Então para encontrar , falta encontrar a tensão normal média .
Para tanto, podemos:
- Fazer um diagrama de corpo livre e aplicar as equações de equilíbrio na peça para encontrar a força normal em função da força ;
- E encontrar a área da seção transversal do vínculo multiplicando a sua espessura pela sua largura .
Passo 2
Começando pelo diagrama de corpo livre de :
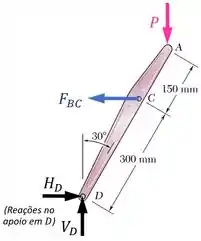
Diagrama de corpo livre feito, agora queremos usar as equações de equilíbrio para relacionar a força , desconhecida, com a força , conhecida.
A única equação de equilíbrio que vai nos permitir fazer isso sem ter que calcular as forças e vai ser o equilíbrio de momentos em relação ao ponto :
Agora vamos pensar...
A força vai gerar um momento no sentido anti-horário, que vamos considerar como positivo ().
Sendo assim, o momento no sentido horário causado pela força vai ficar negativo ().
O braço de vai ser calculado multiplicando a distância de por , enquanto que o braço de vai ser calculado multiplicando a distância de por :
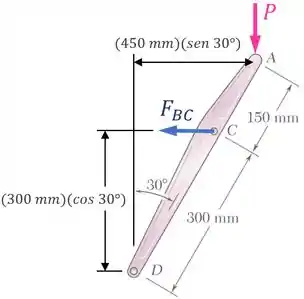
Com tudo isso em mente, o nosso equilíbrio de momentos em relação ao ponto fica assim:
Isolando :
Ok, vamos calcular isso daí...
dividido por dá .
Já dividido por dá:
Então fica assim:
Simplificando:
Pronto, encontramos em função de !
Isso significa que também encontramos a força normal no vínculo em função de , já que :
Passo 3
Com a força normal no vínculo encontrada, podemos agora calcular a tensão normal média :
A área da seção transversal do vínculo é calculada multiplicando a sua espessura pela sua largura . E para a força normal podemos usar a expressão encontrada no passo anterior.
Sendo assim, temos:
Passo 4
Finalmente, podemos fazer o cálculo do fator de segurança :
Substituindo a expressão encontrada para a tensão normal média no último passo:
Passando o “” para cima:
Substituindo os valores , , e :
Agora, calma...
Temos que prestar atenção nas unidades!
Vamos juntar elas em um canto só:
O fator de segurança não tem unidade, então queremos que todas as unidades nessa equação se cortem.
Se reescrevermos como e reescrevermos a força de como , vamos poder cortar todas as unidades:
Cortando as unidades, sobra só os números:
Calculando, isso dá: