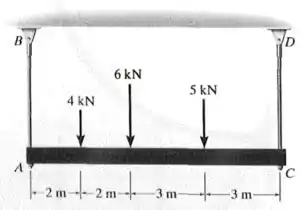
As hastes e são feitas de aço cuja tensão de ruptura por tração é . Usando um fator de segurança para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em e .
Passo 1
O que está acontecendo?
As hastes e estão suportando a viga , garantindo o seu equilíbrio.
Para saber a intensidade das forças de tração feitas pela viga nas hastes, e , precisamos fazer um diagrama de corpo livre da viga (como o da figura abaixo) e aplicar as equações de equilíbrio nela.
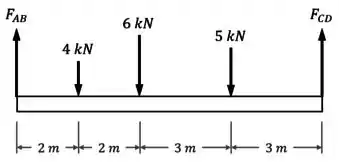
Essas forças de tração e vão gerar forças internas normais e nas hastes.
As forças normais, por sua vez, vão gerar uma tensão normal média em cada haste.
E o que é que o exercício quer?
O exercício quer saber quais são os diâmetros mínimos das hastes para que as trações e não gerem tensões normais médias nelas acima da tensão normal admissível :
Como sempre, a tensão admissível é calculada dividindo a tensão de falha (nesse caso, a tensão de ruptura ) pelo fator de segurança .
Podemos definir e aplicar a condição para as duas hastes de forma genérica. Ao final, devemos isolar o diâmetro e calcular o seu valor duas vezes, uma vez para cada haste.
Passo 2
Vamos começar pelo diagrama de corpo livre da viga:
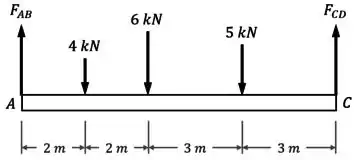
Para encontrar e , precisamos usar as equações de equilíbrio.
Vamos pensar... Nesse caso, temos duas equações de equilíbrio que podemos utilizar: o equilíbrio de momentos e o equilíbrio de forças na vertical.
Começando pelo equilíbrio de momentos... Se fizermos ele em relação ao ponto , ele fica assim:
A força tem um braço de e gera um momento no sentido anti-horário, que vamos considerar como positivo.
Já as forças de , e tem braços de , e , respectivamente, e geram momentos no sentido horário, ou seja, momentos negativos.
Então o nosso somatório de momentos fica assim:
Somando todos os momentos negativos:
Isolando :
Seguindo com o equilíbrio de forças na vertical:
As forças e apontam para cima, enquanto as demais apontam para baixo, então:
Somando as forças negativas:
Isolando e substituindo :
Passo 3
Com as forças de tração determinadas, podemos prosseguir e definir as tensões normais médias nas hastes e :
As forças normais internas nas hastes são iguais às suas respectivas forças de tração .
Já as áreas das seções transversais das hastes devem ser calculadas a partir da área do círculo em função de seu diâmetro : .
Dessa forma, temos que para as duas hastes a tensão normal média é definida por:
Passo 4
Aplicando a condição de projeto:
Podemos substituir pela expressão encontrada no último passo e sabemos que . Dessa forma, temos que:
Como queremos encontrar , devemos isolá-lo:
Espelhando essa equação (para deixar ela mais fácil de visualizar) e fazendo a raiz quadrada dos dois lados:
Agora, o próximo passo é calcular o diâmetro duas vezes. Quando usarmos a força , vamos encontrar o diâmetro , e, quando usarmos , vamos encontrar .
Passo 5
Para a haste :
Substituindo os valores , e :
Como , podemos reescrever a força de como para que o resultado final do diâmetro saia diretamente em :
Calculando a expressão da direita, isso dá:
Para a haste :
Ao substituir os valores de , e , podemos dessa vez já substituir direto em newtons ():
Calculando a expressão da direita: