O elemento está sujeito a uma força de compressão de . Se e forem feitos de madeira e tiverem de espessura, determine, com aproximação de , a menor dimensão do apoio de modo que a tensão de cisalhamento média não exceda .
Passo 1
O que está acontecendo?
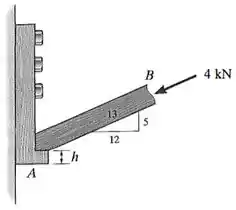
A componente vertical da força de vai ser transmitida até o apoio em , gerando uma força cortante nesse apoio.
Para calcular essa força cortante , vamos ter que calcular o valor da componente vertical da força de e fazer uma análise de esforços internos na seção entre o apoio e o pedaço principal da peça :
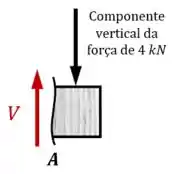
Essa força cortante vai gerar uma tensão cisalhante média no apoio. A área da seção resistente à essa tensão pode ser calculada usando a espessura e a dimensão do apoio.
E o que é que o exercício quer?
O exercício quer que a gente encontre a tensão cisalhante média em função da dimensão do apoio, para que possamos aplicar a condição de projeto:
Substituído o valor de nessa expressão, vamos poder isolar e descobrir qual deve ser o seu valor mínimo, tendo em mente que o seu valor deve ser um múltiplo de .
Passo 2
Vamos começar então calculando o valor da componente vertical da força de ...
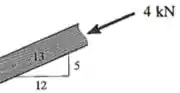
Se observarmos o triângulo de dimensões na figura do exercício:
E observarmos o triângulo formado pela decomposição da força de em uma componente horizontal e uma componente vertical :
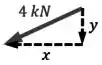
Podemos fazer uma semelhança de triângulos para encontrar a componente vertical .
está para a dimensão assim como está para a dimensão :
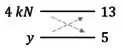
Com isso, encontramos que:
O que significa que a componente vertical vai ser:
Com essa informação em mãos, agora podemos fazer a análise dos esforços internos no apoio:
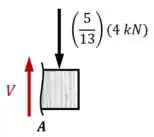
Pelo equilíbrio de forças, temos que:
O que significa que:
Passo 3
O próximo passo é encontrar a tensão cisalhante média :
A área é a área da seção transversal do apoio onde avaliamos anteriormente os esforços internos:

Essa seção é retangular, de base e altura .
Isso significa que , de tal forma que:
Passo 4
encontrado, agora podemos aplicar a condição de projeto:
Substituindo o valor de :
Como queremos encontrar o valor de , devemos isolá-lo:
Espelhando a expressão (para que ela fique mais fácil de visualizar) e substituindo os valores de , e :
Antes de calcular isso, vamos tomar cuidado com as unidades!
Como , se reescrevermos a força de como , vamos estar trabalhando só com as unidades e , o que vai facilitar nossa vida:
Calculando a expressão da direita, isso dá:
Como deve ser dado em múltiplos de , então temos que o valor mínimo de de modo que a tensão cisalhante média não exceda é: