Determine a intensidade da carga distribuída máxima que pode ser suportada pelo conjunto de pendural de modo a não ultrapassar uma tensão de cisalhamento admissível de nos parafusos de de diâmetro em e e uma tensão de tração admissível de na haste de de diâmetro.
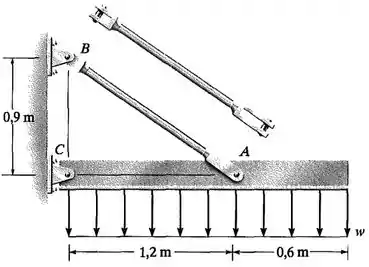
Passo 1
O equilíbrio da viga, quando ela está submetida à força distribuída , se dá através:
- De uma força transmitida pela haste ao longo de seu comprimento;
- E das forças de reação vertical e horizontal no apoio em .
Como mostra o diagrama de corpo livre da viga:
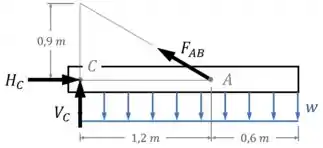
E a haste? O que acontece com ela?
Quando a haste transmite essa força desde o apoio em até a viga em , ela acaba tendo que resistir a essa força de duas formas:
1. Os parafusos em e tem que transmitir a força em condição de cisalhamento duplo:
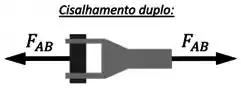
Se lembrarmos de quando estudamos cisalhamento duplo, vamos nos lembrar que isso significa que a força cortante nos parafusos é igual a metade da força transmitida:
Essa força cortante vai gerar uma tensão cisalhante média nos parafusos que não pode ultrapassar a tensão de cisalhamento admissível .
2. A haste é tracionada pela força , o que gera nela uma força normal , o que gera uma tensão normal média que não pode ultrapassar a tensão normal admissível .
Os diâmetros fornecidos e vão ser úteis para que a gente possa calcular as áreas das seções transversais dos parafusos e da haste.
E o que é que o exercício quer?
Ele quer saber qual é o valor máximo da carga distribuída tal que as condições:
ainda sejam satisfeitas.
A partir de um certo valor, a força vai gerar tensões maiores que as tensões admissíveis.
O que nós vamos fazer é aplicar essas duas condições acima para encontrar qual é o valor máximo permitido de .
A partir do valor máximo permitido de , vamos aplicar as equações de equilíbrio na viga para encontrar qual é o valor de correspondente.
Passo 2
Vamos começar então calculando os valores máximos permitidos para .
1. Para a tensão cisalhante média nos parafusos, temos:
Usando a fórmula da tensão cisalhante média isso fica:
A área da seção transversal dos parafusos pode ser calculada em função do diâmetro usando a fórmula .
Além disso, os parafusos estão sob cisalhamento duplo por uma força . Isso significa que a força cortante é igual à metade de .
Usando tudo isso, a expressão anterior fica assim:
Isolando :
Substituindo e :
Como , o resultado desse cálculo vai sair em . Fazendo o cálculo, isso dá:
2. E agora para a tensão normal média na haste:
Usando a fórmula da tensão normal média :
A haste está sob uma tração de intensidade , então . Além disso, podemos calcular a área da seção transversal da haste a partir de seu diâmetro . Dessa forma, temos:
Isolando :
Substituindo e :
Mais uma vez, , o que significa que o nosso resultado sai em newtons ():
Comparando os dois valores máximos permitidos para :
- para a falha dos parafusos por cisalhamento;
- E para a falha da haste por tensão normal.
vemos que o menor valor permitido é:
Passo 3
Agora que temos o valor máximo permitido para , precisamos achar o valor correspondente de .
Para fazer isso, vamos observar diagrama de corpo livre da viga:
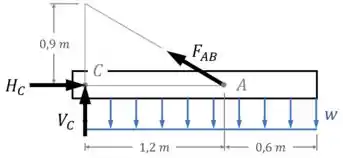
Podemos usar as equações de equilíbrio para encontrar em função de .
A equação de equilíbrio que nos permite fazer isso mais facilmente vai ser o equilíbrio de momentos em relação ao ponto :
As únicas forças que geram momentos em relação a esse ponto são a força distribuída e a força .
Vamos fazer uma pausa para analisar esses momentos...
Se você souber calcular esses momentos, pode pular essa pausa. É só procurar pelo “Voltando para o equilíbrio de momentos...” um pouco abaixo! :)
Quanto a força :
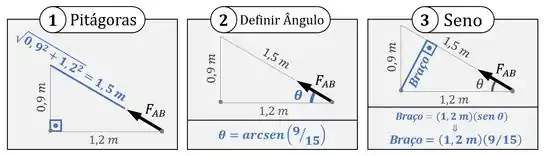
A força vai gerar um momento no sentido anti-horário () e vai ter um braço de , como mostra a figura abaixo:
Quanto a força distribuída :
Lembra aí!
Quando aprendemos forças distribuídas, vimos que a resultante de uma força distribuída uniforme age bem no meio da região onde a força distribuída está.
Além disso, a intensidade dessa resultante é igual a intensidade da força distribuída (, nesse caso) vezes o comprimento em que ela atua (, nesse caso).
Dessa forma, o momento gerado por vai ser igual a intensidade da resultante vezes o braço de .
Além disso, o momento gerado por vai estar no sentido horário ().
Voltando para o equilíbrio de momentos...
Tendo tudo o que vimos em mente, o equilíbrio de momentos fica assim:
Isolando :
Calculando, isso dá:
Passo 4
Agora podemos juntar a expressão que acabamos de achar:
Com o valor máximo permitido para , :
Arrumando as unidades, fica assim:
Calculando, isso dá:
Esse resultado é um pouco grande, então podemos reescrevê-lo em :