Abaixo é dado uma treliça plana. Determine as tensões normais e cisalhantes que ocorrem na Barra AD, no plano 39°. Todas as barras são quadradas com seção (40x40)cm.
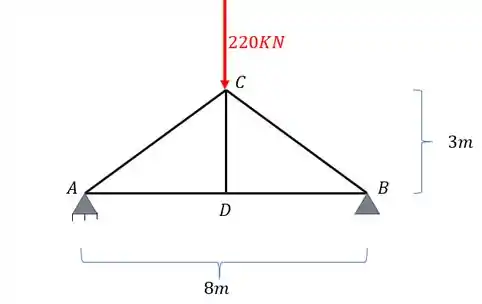
Passo 1
Antes de qualquer conta precisamos o passo a passo de solução do nosso problema. Por se tratar de uma treliça plana sabemos que os únicos esforços que apareceram são os esforços normais. Como queremos calcular só uma barra, calculamos o valor do normal nela. Depois que fizermos isso teremos uma barra com um esforço normal, basta decompor ele no plano a 39° e fazer a conta para as tensões que já sabemos que tem as seguintes fórmulas
Vamos lá então.
Passo 2
Vamos primeiro descobri o normal na nossa barra resolvendo a nossa treliça.
Primeiro calculamos as reações dos apoios
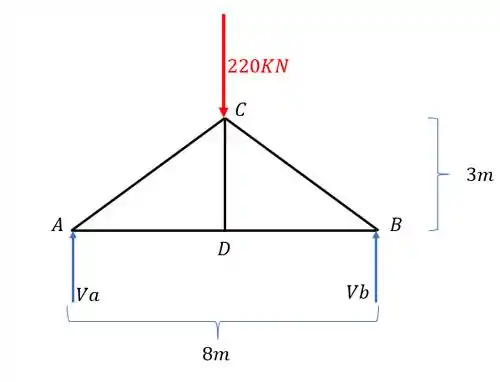
Fazendo o somatório de momentos igual a zero no ponto A teremos que
Por consequência teremos que
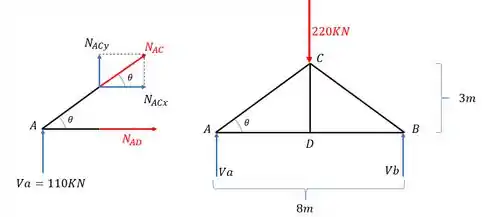
Como já temos as reações de apoio, vamos fazer o equilíbrio de forças no nó A
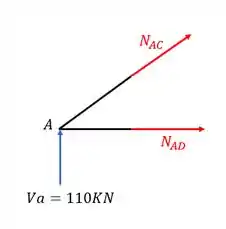
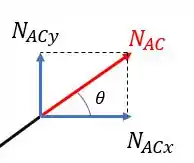
Precisamos agora decompor o normal
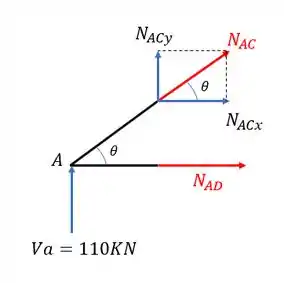
Mas como determinamos esse ?
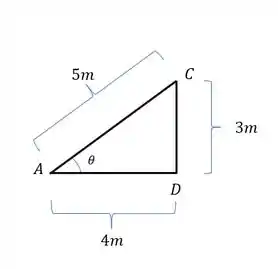
Com isso podemos determinar as relações trigonométricas do nosso triangulo
Passo 3
Vamos fazer a decomposição do nosso normal agora
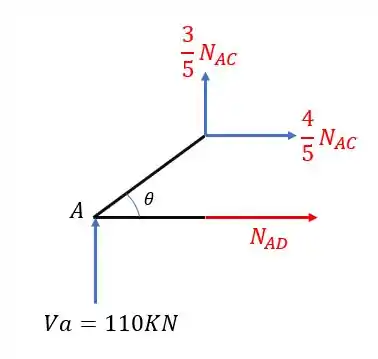
se fizermos o equilíbrio da nossa peça teremos que
Resolvendo o primeiro sistema teremos que
Passo 4
Agora que já temos o nosso carregamento, vamos analisar a nossa barra
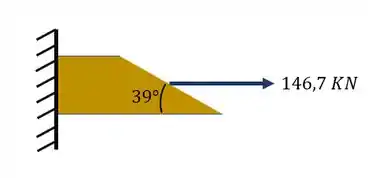
Agora já sabemos o plano que está agindo assim como o carregamento. Agora precisamos fazer uma decomposição de vetores. Um vetor será perpendicular ao plano, ou seja, normal ao plano, logo podemos calcular com ele a nossa tensão normal. O outro vetor será paralelo ao plano, ou podemos dizer que causará um esforço cortante, nesse caso essa força nos dará a tensão cisalhante. Dessa forma teremos que

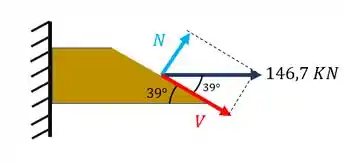
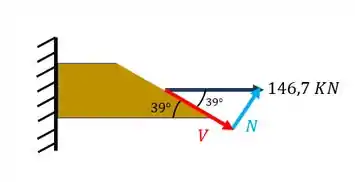
Fazendo a decomposição de forças teremos que
Passo 5
Agora que já temos os esforços, falta determinarmos as tensões, sabemos que a fórmula para tensão é
Mas temos que tomar muito cuidado, porque essa área não é da seção transversal, mas da seção do plano orientado a 39°, como calcularemos essa área?
Basta apenas olharmos a seção da seguinte maneira
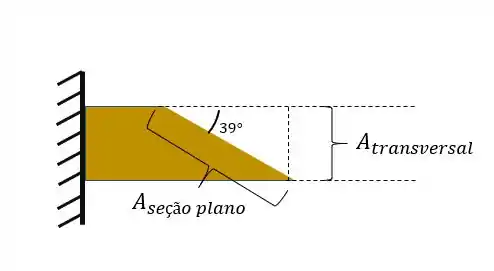
Podemos ver que a relação entre área transversal e área da seção pode se dar por uma relação trigonométrica.
No enunciado é dito que a seção da nossa peça é 40x40 cm, logo teremos que
Substituindo na nossa equação teremos que
Passo 6
Agora só precisamos determinar as nossas tensões, temos que
Substituindo