Um corpo de prova sob tração com área de seção transversal é submetido a uma força axial . Determine a tensão de cisalhamento média máxima no corpo de prova e indique a orientação de uma seção na qual ela ocorre.

Passo 1
O que está acontecendo?
Dependendo da orientação de uma seção qualquer desse corpo de prova, essa seção vai ter:
- Uma certa força interna cortante , calculada a partir da força externa e do ângulo através de uma análise de esforços internos na seção;
- E uma certa área , calculada a partir do ângulo e da área da seção transversal do corpo de prova.
Então dependendo da orientação de uma seção qualquer do corpo, essa seção vai ter uma certa tensão cisalhante média .
E o que é que o exercício quer?
Ele quer que a gente descubra:
- A tensão cisalhante média máxima nessa peça;
- E a orientação de uma seção onde essa tensão máxima ocorre.
Para fazer isso, temos que calcular , e em função do ângulo .
Daí, vamos poder ver em função de como uma função:
para, em seguida, analisar os máximos dessa função.
Passo 2
Vamos começar calculando a força cortante em função do ângulo .
Fazendo uma análise de esforços internos em uma seção qualquer, vamos encontrar uma força normal e uma força cortante .
Para o equilíbrio das peças, a resultante dessas forças internas e deve ser igual à força externa :
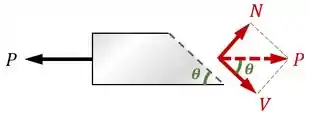
Desenhando corretamente o ângulo nessa figura acima e usando seno & cosseno, encontramos que:
Passo 3
Precisamos calcular também a área de uma seção qualquer em função da sua orientação .
Podemos usar o ângulo para relacionar a área da seção qualquer com a área da seção transversal:
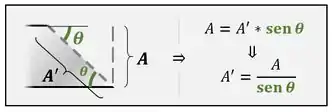
Assim, obtemos que:
Passo 4
Agora que e foram calculados para uma seção qualquer em função da sua orientação , podemos calcular a tensão cisalhante média em função de :
Aplicando a fórmula da tensão cisalhante média para a seção qualquer:
Substituindo as expressões encontradas para e nos passos anteriores:
Reorganizando essa expressão, temos:
Passo 5
Agora que temos a função , precisamos analisar os seus máximos para encontrar .
Para fazer isso, vamos nos lembrar um pouco de cálculo...
Uma função tem seus pontos críticos (pontos de máximo ou de mínimo) quando a sua primeira derivada é igual a zero.
Aplicando isso para a nossa função, temos:
Substituindo a expressão que tínhamos encontrado para :
Como e são constantes, podemos tirar esses termos da derivada:
Dividindo os dois lados por , esses termos somem:
Sabendo que:
- (Regra do Produto);
- ;
- E ,
Essa derivada fica assim:
O que significa que:
O primeiro ângulo com seno e cosseno iguais que conhecemos é o ângulo de .
O que significa que é a orientação de uma seção em que a tensão cisalhante é máxima!
Passo 6
Agora, voltamos para a expressão encontrada para e substituímos para encontrar :
Substituindo :
Como :
O que dá: