Um tubo de aço com de diâmetro externo é fabricado a partir de uma chapa de aço com espessura de soldada ao longo de uma hélice que forma um ângulo de com um plano perpendicular ao eixo do tubo. Sabendo que as tensões normal e de cisalhamento máximas admissíveis nas direções, respectivamente, normal e tangencial à solda são e , determine a intensidade da maior força axial que pode ser aplicada ao tubo.
Passo 1
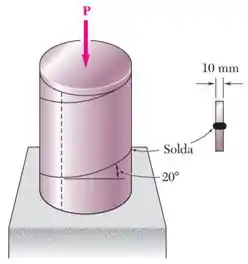
A solda nesse tubo foi feita no formato de uma “rampa em espiral”, formando um ângulo em relação ao plano horizontal.
Além disso, essa solda tem um diâmetro externo , uma espessura , e, consequentemente, um diâmetro interno .
E o que é que o exercício quer?
O exercício quer saber qual é a maior força que pode ser feita no tubo tal que as tensões na solda não ultrapassem os seus valores admissíveis de:
- para a tensão normal ;
- E para a tensão cisalhante .
Precisamos então estudar como afeta as tensões normal e cisalhante na região da solda para descobrir, a partir dos valores admissíveis das tensões, o valor máximo permitido de .
Agora... Para estudar as tensões na região da solda, não podemos estudar a solda inteira, já que a gente não sabe o tamanho total dela.
Então ao invés de estudar a solda inteira, vamos estudar só uma revolução da solda:
Vamos calcular a área da superfície de uma revolução da solda.
Calcular os esforços internos resultantes normal e cortante em uma revolução da solda.
E calcular as tensões normal média e cisalhante média em uma revolução da solda.
Passo 2
Vamos começar então calculando a área da superfície de uma revolução da solda.
A área da seção transversal do tubo pode ser calculada como a diferença entre as áreas de um círculo de diâmetro e outro menor de diâmetro :
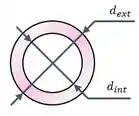
Como a área de um círculo em função de seu diâmetro é dada por , então a área fica assim:
Deixando em evidência, temos:
Agora temos que, de alguma forma, relacionar essa área com a área da superfície de uma revolução da solda.
Para fazer isso, vamos “desenrolar” uma revolução do tubo:
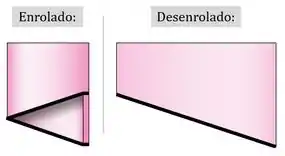
Ao fazer isso, a área passa a ser a área da seção horizontal, enquanto a área é a área da seção inclinada :
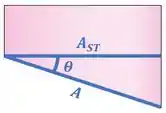
Daí tiramos que:
Isolando a área , temos:
Substituindo a expressão encontrada para :
Passo 3
O próximo passo é encontrar as forças internas resultantes normal e cortante em uma revolução da solda.
Para fazer isso, vamos mais uma vez usar o tubo “desenrolado”, dessa vez vendo os esforços internos na região da solda:
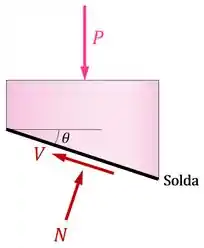
Para o equilíbrio desse pedaço do tubo, precisamos que a resultante das forças e tenha a mesma intensidade da força , mas sentido oposto:

Dessa imagem, conseguimos tirar que:
E que:
Passo 4
Agora que encontramos , e para uma revolução da solda, podemos encontrar as tensões nessa região e, em seguida, calcular a força correspondente à cada tensão admissível.
Primeiro, vamos fazer esse processo com a tensão normal .
Aplicando a fórmula da tensão normal média:
Substituindo as expressões encontradas nos dois passos anteriores:
Passando o para cima:
Como queremos encontrar o valor de correspondente a um certo valor de , vamos isolar :
Agora podemos substituir os valores:
- ;
- ;
- ;
- E .
- ;
- ;
- ;
- E .
Fazendo isso, temos:
Como , o resultado dessa conta vai sair em newtons ().
Calculando tudo, isso dá:
Como esse número está um pouco grande, reescrevemos ele em :
Isso significa que uma carga de gera na solda a tensão normal admissível de . Qualquer carga maior do que não é permitida nesse tubo.
Passo 5
Agora podemos fazer o mesmo procedimento do passo anterior mas para a tensão cisalhante .
Aplicando a fórmula da tensão cisalhante média:
Substituindo as expressões encontradas para a força cortante e para a área da seção:
Passando o para cima:
Como queremos encontrar o valor de correspondente a um certo valor de , vamos isolar :
Agora podemos substituir os valores:
Fazendo isso, temos:
Calculando tudo e sabendo que , isso dá:
Reescrevendo em :
Ou seja, a tensão cisalhante admissível requer que a força não ultrapasse o valor de .
Em comparação, não são permitidas forças maiores que de acordo com a tensão normal admissível .
Sendo assim, a maior força que pode ser feita no tubo é: