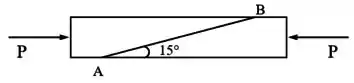
Duas peças de madeira de seção são coladas na seção inclinada como mostra a figura.
Calcular o valor máximo admissível da carga , axial de compressão, dadas as tensões admissíveis na cola de à compressão e ao cisalhamento.
Dica do Expert: e .
Passo 1
Nós precisamos descobrir qual é a máxima carga de compressão nas peças tal que as tensões na cola não ultrapassem os seus valores admissíveis:
- para a tensão normal ;
- E para a tensão cisalhante .
E como podemos fazer isso?
Vamos pensar...
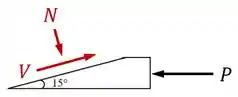
Cada carga vai gerar uma certa força normal e uma certa força cortante na seção inclinada da cola:
Além disso, a seção inclinada da cola possui uma área que é diferente da área de da seção transversal das peças de madeira:
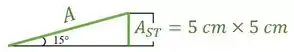
Se encontrarmos as forças e , em função da carga , e a área da seção da cola, podemos usar as fórmulas das tensões normal média e cisalhante média :
Para encontrar as tensões na seção da cola em função da carga .
A partir daí, podemos descobrir qual é a carga que gera uma tensão normal e qual é a carga que gera uma tensão cisalhante .
O menor entre esses dois valores de vai ser a nossa resposta, já que qualquer valor maior geraria pelo menos uma tensão acima da admissível.
Passo 2
Então primeiro, vamos observar os esforços internos na seção da cola para encontrar as forças normal e cortante em função da carga :
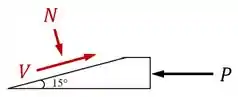
Para o equilíbrio dessa peça, a resultante das forças internas e tem que ter a mesma intensidade da força externa e sentido oposto:
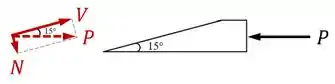
Como é o ângulo entre a horizontal (onde a carga atua) e a seção inclinada (onde a cortante atua), podemos desenhar esse ângulo no diagrama de forças e usar seno e cosseno para obtermos que:
Passo 3
Em seguida, vamos encontrar a área da seção da cola.
Se observamos a geometria das peças, conseguimos relacionar a área dessa seção inclinada com a área da seção transversal das peças:
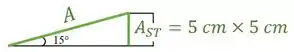
Como seno é o cateto oposto sobre a hipotenusa:
Isolando a área , temos que:
Passo 4
Agora que , e foram encontrados para a seção da cola, podemos usar as fórmulas das tensões normal média e cisalhante média para essa seção:
Substituindo os valores encontrados nos últimos dois passos:
Passando o que está dividindo a área para cima, essas tensões ficam assim:
Passo 5
Para descobrir qual é o valor de que gera uma tensão normal de na seção da cola, partimos da expressão que encontramos no passo anterior:
Isolamos :
E substituímos os valores de , , e :
Lembra aí! , então o resultado desses cálculos vai sair em newtons!
Calculando tudo, obtemos que:
Esse número é um pouco grande, então podemos reescrevê-lo em :
Ou seja, a tensão normal admissível permite cargas de até .
Passo 6
Para descobrir o valor de que gera uma tensão cisalhante na seção da cola, partimos da outra expressão que encontramos no passo 4:
Isolamos :
E substituímos os valores de , , e :
Calculando isso e sabendo que , obtemos:
Reescrevendo em :
Ou seja, a tensão cisalhante admissível requer que a carga não ultrapasse o valor de . Em comparação a tensão normal admissível permite cargas de até !
Então a tensão cisalhante admissível é o fator limitante e o valor máximo admissível da carga é: