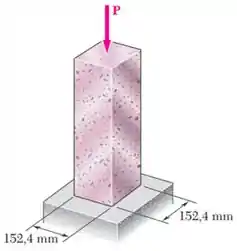
Uma carga de é aplicada ao bloco de granito mostrado na figura. Determine o valor máximo resultante da () tensão normal e () tensão de cisalhamento. Especifique a orientação do plano no qual ocorre cada um desses valores máximos.
Passo 1
Para descobrir os valores máximos resultantes () da tensão normal média e () da tensão cisalhante média nesse bloco de granito, vamos ter que:
1. Calcular essas tensões para uma seção qualquer do bloco.
Podemos fazer isso:
- Definindo uma seção com uma orientação qualquer ;
- Usando as fórmulas e para calcular as tensões nessa seção qualquer;
- E tomando cuidado para calcular as forças internas normal e cortante e a área da seção de acordo com a orientação dessa seção qualquer.
Além disso, para calcular as forças internas e , vamos usar a informação de que a carga aplicada no bloco é de .
E para calcular a área da seção qualquer, vamos precisar da área da seção transversal do bloco.
2. Estudar os valores máximos das expressões que encontrarmos no passo anterior.
Passo 2
Vamos começar encontrando as forças internas e para uma seção qualquer de orientação :
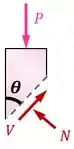
Para o equilíbrio interno do bloco de granito, a resultante dessas duas forças deve ter sempre uma intensidade igual à carga e um sentido contrário:
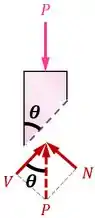
Dessa imagem, tiramos que:
Passo 3
Em seguida, podemos encontrar a área de uma seção qualquer em função da área da seção transversal:
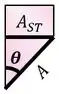
Dessa imagem, tiramos que , o que significa que:
Passo 4
, e calculados para uma seção qualquer, agora podemos calculas as tensões em uma seção qualquer.
Começando pela tensão normal média :
Substituindo os valores encontrados para e :
Passando o que está dividindo para cima:
E agora para a tensão cisalhante média :
Substituindo os valores encontrados para e :
Mais uma vez, passando o que está dividindo para cima:
Passo 5
Tanto quanto tem “” em comum, então já podemos deixar esse termo calculado.
Sabendo que e :
Para ter resultados em , podemos reescrever a força de em newtons ():
Calculando, isso dá:
Sendo assim, podemos escrever as tensões e assim:
Passo 6
Enfim, podemos estudar os valores máximos das expressões que encontramos para as tensões e no passo anterior.
Começando pela tensão normal média :
Ela vai ser máxima quando for máximo.
O valor máximo que pode ter é , e isso acontece quando , então temos que a tensão normal média máxima nesse bloco é:
E agora para a tensão cisalhante média :
Ela vai ser máxima quando for máximo.
Para saber quando é máximo, temos que usar um pouco de cálculo.
Em cálculo, vimos que os valores máximos e mínimos de uma função ocorrem quando sua derivada é igual a zero.
Aplicando isso para , temos:
Usando a regra do produto para derivadas e sabendo que derivada de seno é cosseno e derivada de cosseno é menos seno, essa derivada fica assim:
O que significa que:
O primeiro ângulo com seno e cosseno iguais que conhecemos é o ângulo de .
Isso significa que é a orientação de uma seção em que a tensão cisalhante é máxima!
Sendo assim:
Como , temos que , o que significa que:
O que dá:
E assim chegamos às respostas do exercício:
Resposta
() . Ocorre no plano normal do bloco. ( em relação à vertical)
() . Ocorre em um plano com uma angulação em relação à vertical.