A estrutura de dois elementos está sujeita à carga distribuída mostrada. Determine a maior intensidade da carga uniforme que pode ser aplicada à estrutura sem que a tensão normal média ou a tensão de cisalhamento média na seção ultrapasse e , respectivamente. O elemento tem seção transversal quadrada de de lado.
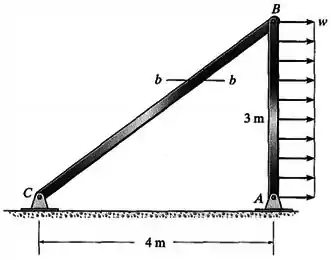
Passo 1
A haste faz uma força na viga que contribui para o equilíbrio da viga, como mostra o diagrama de corpo livre da viga:
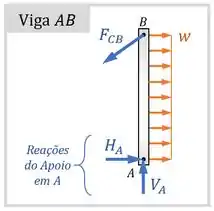
Como reação, a viga traciona a haste com uma força de mesma intensidade:
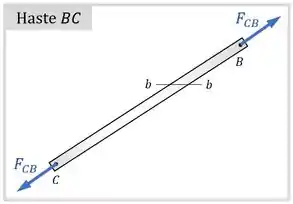
Isso significa que podemos usar as equações de equilíbrio na viga para descobrir o valor da tração na haste.
Sabendo o valor da tração na haste, podemos calcular os esforços internos normal e cortante na seção da haste:
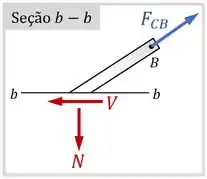
Além disso, sabendo que a haste possui uma seção transversal de área , podemos calcular também a área da seção a partir da inclinação da haste:
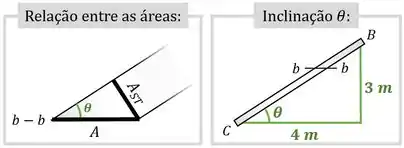
Sabendo os valores de , e para a seção , podemos calcular também as tensões normal média e cisalhante média nessa seção através de suas fórmulas:
Essas tensões e vão estar, no final das contas, em função da intensidade desconhecida da carga distribuída.
Comparando essas tensões com as tensões máximas permitidas e , vamos poder descobrir os valores correspondentes de .
O menor entre os dois valores encontrados vai ser o valor máximo permitido para , que é o que o exercício quer!
Passo 2
Vamos começar então encontrando a força de tração na haste.
Para tanto, podemos fazer um diagrama de corpo livre (“DCL”) da viga para poder relacionar a força com a intensidade da carga distribuída:
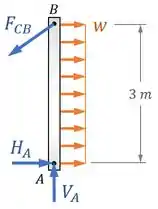
Para deixar nossa vida mais fácil, substituímos a carga uniforme de intensidade , que age em uma região de , por uma força equivalente que age no centro dessa região:
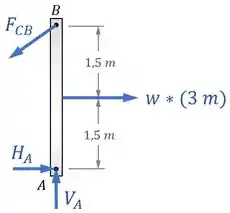
Agora, podemos aplicar uma condição de equilíbrio para tentar relacionar e .
A condição de equilíbrio que vai nos permitir relacionar esses valores mais facilmente vai ser o equilíbrio de momentos em relação ao ponto :
Agora vamos pensar...
A força vai gerar em relação ao ponto um momento no sentido horário () com um braço de .
Quanto a força , não está muito claro qual é o braço dessa força.
Para ficar mais fácil de calcular o momento gerado por , podemos decompor essa força usando a inclinação da haste:
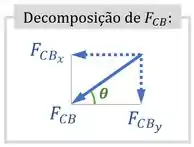
Dessa forma, podemos calcular os momentos gerados pelas componentes de :
- A componente vertical não vai gerar nenhum momento em relação ao ponto (ela vai ter um braço ).
- E a componente vai gerar um momento no sentido anti-horário () com um braço de .
Além disso, da decomposição de , temos que:
Voltando para o nosso equilíbrio de momentos:
Tendo em mente o que acabamos de ver, esse equilíbrio de momentos fica assim:
Dividindo tudo por :
Passando para o outro lado, temos que:
E usando a relação de que , encontramos a outra componente de :
Como temos as duas componentes, já podemos dizer que encontramos a força .
Passo 3
Agora que temos a força de tração na haste, podemos avaliar os esforços internos na seção :
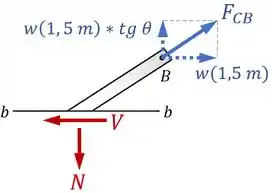
A vantagem de ter deixado a força já decomposta no passo anterior é que agora fica fácil encontrar as forças internas normal e cortante .
Aplicando o equilíbrio de forças na vertical e na horizontal:
Encontramos que:
Passo 4
Em seguida, precisamos encontrar a área da seção .
Usando a inclinação da haste para relacionar essa área com a área da seção transversal da haste:
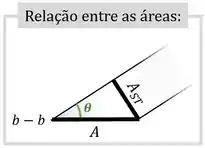
Encontramos que:
Isolando a área , temos que:
Passo 5
Agora que encontramos as forças internas e e a área da seção , podemos calcular as tensões nessa seção.
Aplicando a fórmula da tensão normal média, temos:
Substituindo os valores encontrados para e :
Passando o para cima:
E agora para a tensão cisalhante média:
Substituindo os valores encontrados:
Passando o para cima:
Passo 6
Mas, na verdade, queremos descobrir os valores de correspondentes a certas tensões e .
Então vamos isolar nas expressões que encontramos no último passo.
Começando pela tensão normal média:
Isolando , temos:
Conhecemos a tensão normal máxima permitida na seção , , e a área da seção transversal da haste .
Mas ainda precisamos descobrir os valores de e de .
Para tanto, vamos olhar para a inclinação da haste:
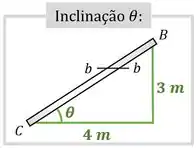
Dessa imagem, conseguimos tirar que:
Além disso, sabemos que é igual ao cateto oposto de dividido pela hipotenusa, que pode ser encontrada pelo teorema de Pitágoras:
Substituindo todos esses valores na expressão anterior para :
Empurrando todas as unidade para o lado:
Como , então , o que significa que o resultado desses cálculos vai sair em .
Calculando tudo, isso dá:
Como esse número é um pouco grande, reescrevemos ele em :
Isso significa que a tensão normal máxima permitida na seção da haste implica que só podem ser aplicadas na viga cargas distribuídas de até .
Agora para a tensão cisalhante média:
Isolando , temos:
Substituindo a tensão cisalhante máxima permitida , a área e o valor encontrado para , temos:
Mais uma vez, o resultado de tudo isso vai sair em . Calculando tudo, isso dá:
Reescrevendo em :
Ou seja, a tensão cisalhante máxima permitida na seção da haste implica que só podem ser aplicadas na viga cargas distribuídas de até .
Sendo assim, a tensão cisalhante é o fator limitante e a maior intensidade da carga uniforme que pode ser aplicada à estrutura é: