Uma barra de madeira de seção (30x30)cm está sujeita aos esforços mostrados abaixo. Usando seus conhecimentos de tensões normais e cisalhantes médias, determine as tensões que aparecem no plano indicado na figura. Atente-se para calcular as tensões no ponto indicado pelo plano.
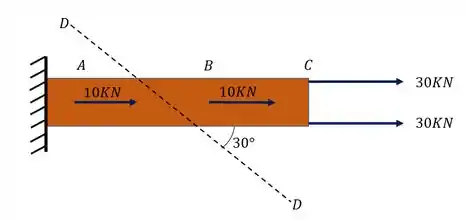
Passo 1
Para resolver essa questão temos que tomar alguns cuidados. O primeiro é colocar todas as cargas fora do centro, no centro da peça, isso vai facilitar as contas que estamos fazendo.
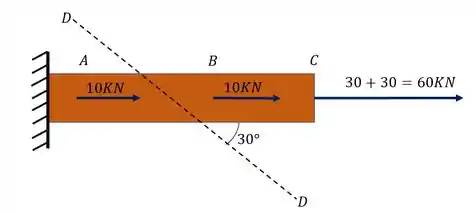
Em seguida devemos destacar o plano que estaremos calculando as tensões, isso é importante pois é exatamente esse o objetivo da questão, logo temos que ter certeza de onde estamos fazendo a conta.
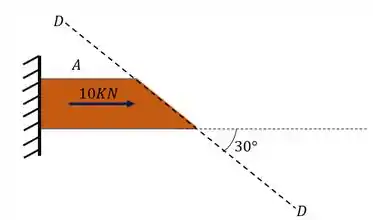
Passo 2
Agora já sabemos qual o plano que devemos calcular, assim como a sua orientação, mas que forças agem nele?
É bem fácil pegar esse esquema, é só você olhar a imagem anterior e se perguntar o seguinte. Quais forças estão faltando? Ou seja, que forças eu estava aplicando na minha peça e que não estão mais aparecendo? Serão exatamente essas forças que estarão agindo no nosso plano, e elas estão representadas aqui em baixo
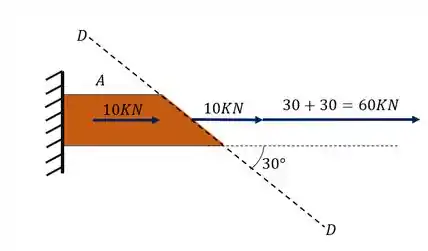
Mas e aquele 10KN que sempre esteve antes do plano que estamos calculando?
Ele não entrará na conta, pois pelo nosso macete, só estará agindo no plano as forças que eu tirei quando destaquei o nosso plano D-D, isso é uma pegadinha, se você estiver distraído pode acabar somando esse 10 KN sem querer, então toma cuidado com isso.
Como só temos esses dois carregamentos agindo vamos transforma-los em um único vetor.
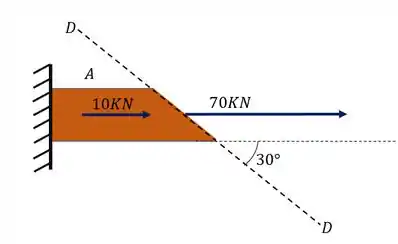
Passo 3
Agora já sabemos o plano que está agindo assim como o carregamento. Agora precisamos fazer uma decomposição de vetores. Um vetor será perpendicular ao plano, ou seja, normal ao plano, logo podemos calcular com ele a nossa tensão normal. O outro vetor será paralelo ao plano, ou podemos dizer que causará um esforço cortante, nesse caso essa força nos dará a tensão cisalhante. Dessa forma teremos que
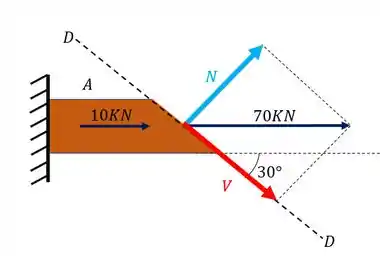
E qual será o ângulo entre esses vetores? Basta usarmos a orientação do nosso plano, a sequência de passos abaixo nos mostra como fazer isso
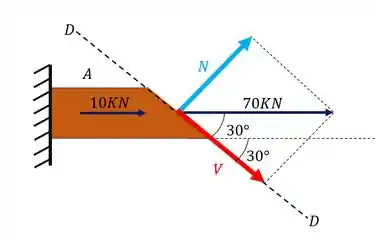
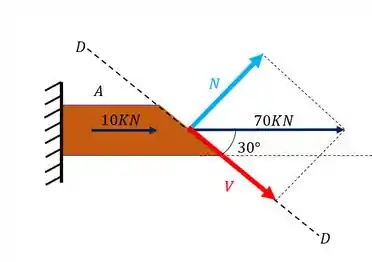
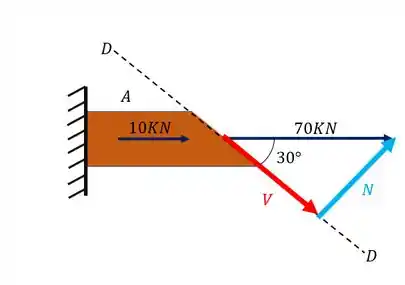
Agora precisamos calcular os esforços normais e cisalhantes pela trigonometria do nosso triangulo. Logo teremos que
Passo 4
Agora que já temos os esforços, falta determinarmos as tensões, sabemos que a fórmula para tensão é
Mas temos que tomar muito cuidado, porque essa área não é da seção transversal, mas da seção do plano orientado a 30°, como calcularemos essa área?
Basta apenas olharmos a seção da seguinte maneira
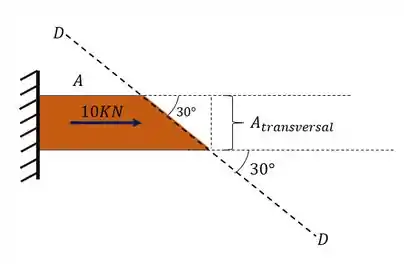
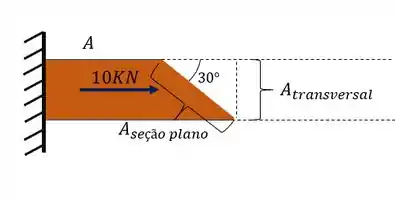
Podemos ver que a relação entre área transversal e área da seção pode se dar por uma relação trigonométrica.
No enunciado é dito que a seção da nossa peça é 30x30 cm, logo teremos que
Substituindo na nossa equação teremos que
Passo 5
Agora só precisamos determinar as nossas tensões, temos que
Substituindo