A barra de aço abaixo foi sujeita ao carregamento indicado. Sabendo que além disso essa barra também sofreu uma variação de temperatura de 40°C, determine qual será o valor das reações da parede para essa peça.
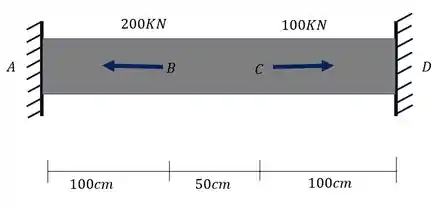
Passo 1
Como podemos ver precisamos analisar duas coisas, a primeira sabemos de cara pelo enunciado, teremos deformações térmicas e tensões térmicas.
Sabemos que podemos calcular as nossas deformações térmicas pela fórmula
E essa fórmula entrará na nossa deformação total máxima.
Além disso também devemos ver se temos um problema estaticamente indeterminado.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá

Fazendo o somatório de forças teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação do trecho AD é composto de quatro parcelas, uma do trecho AB, uma do trecho BC, uma do trecho CD e por fim uma parcela da deformação térmica . Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Por fim sabemos quanto vale a variação de temperatura e o coeficiente de deformação térmica. Então o que falta é apenas determinar o valor dos normais.
Passo 3
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB
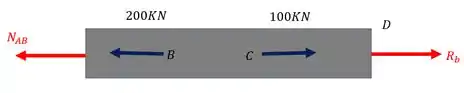
Fazendo o equilíbrio teremos que
Normal do trecho BC

Fazendo o equilíbrio teremos que
Normal do trecho CD
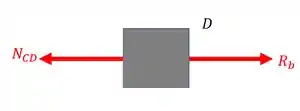
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos multiplicar tudo por EA
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de