A chave elétrica fecha quando as hastes de ligação e se aquecem, o que provoca a translação e a rotação do braço rígido até fechar o contato em . A posição original de é vertical e a temperatura é . Se for feita de bronze C86100 e , de alumínio 6061-T6, determine o espaço exigido entre os contatos para a chave fechar quando a temperatura alcançar .
Dados: , .
Passo 1
O que está acontecendo?
As hastes e , ambas de comprimento inicial , possuem uma temperatura inicial .
Ao serem submetidas a uma variação de temperatura , as barras sofrem uma variação de comprimento térmica que é dada pela fórmula:
Mas as hastes e possuem coeficientes de dilatação térmica diferentes:
- A haste é feita de um bronze para o qual ;
- E a haste é feita de um alumínio para o qual ,
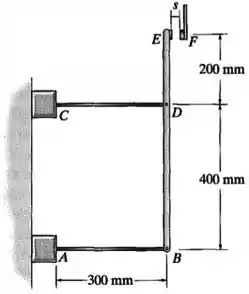
Por causa disso, cada haste vai sofrer uma dilatação térmica diferente, o que vai fazer com que o braço rígido ande para a frente e se incline:
E o que é que o exercício quer?
Ele quer saber qual é a distância entre os pontos e para que eles se encostem quando as hastes e forem aquecidas até uma temperatura final .
Para tanto, teremos que encontrar as dilatações térmicas e em cada haste.
Feito isso, desenharemos a configuração final da barra rígida após a variação de temperatura nas hastes.
Com isso, vamos conseguir avaliar qual deve ser o valor da distância para que a posição final do ponto , o ponto , coincida com o ponto .
Passo 2
Então vamos começar o exercício calculando as dilatações térmicas em cada haste.
Calculando a dilatação térmica da haste , que é de bronze, temos:
Substituindo:
- ;
- ;
- E ,
Vamos encontrar que:
Já a dilatação térmica da haste , que é de alumínio, vai ser:
Substituindo nessa expressão:
- ;
- ;
- E ,
Encontramos que:
Passo 3
O próximo passo é avaliar como vai ficar a barra rígida depois que as hastes tiverem dilatado.
Então vamos pensar...
Sabemos que a barra vai se movimentar como imaginamos na figura do passo 1, já que a dilatação da barra é maior.
E o que é que queremos...
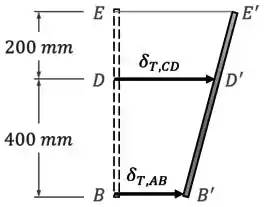
Queremos que a posição final do ponto coincida com o ponto para que a chave elétrica feche.
Então vamos ter que o deslocamento do ponto da barra tem que ser igual à distância inicial entre os pontos e :
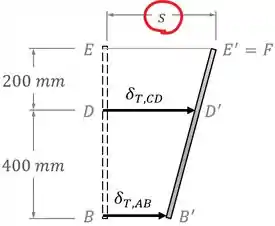
Passo 4
Finalmente, podemos tentar encontrar o valor da distância .
Para tanto, precisamos observar os triângulos formados pela barra em sua posição final:
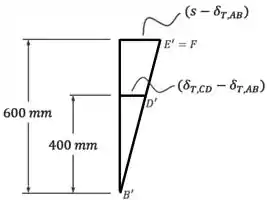
Fazendo uma semelhança de triângulos entre o triângulo menor e o triângulo maior, vamos ter que:
Simplificando os termos que estão dividindo, isso fica assim:
Isolando , temos:
Em seguida, isolando a distância , encontramos:
Finalmente, fazendo a distributiva e simplificando tudo, encontramos que:
Com isso, só falta substituir os valores das dilatações térmicas para encontrarmos o valor da distância !
Substituindo e , vamos ter que:
O que dá a nossa resposta: