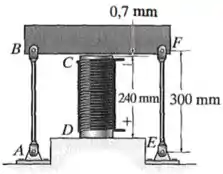
A haste central do conjunto é aquecida de até por resistência elétrica. As duas hastes e situadas nas extremidades também são aquecidas de até . Na temperatura mais baixa, , a folga entre e a barra rígida é . Determine a força nas hastes e provocada pelo aumento na temperatura. As hastes e são feitas de aço e cada uma tem área de seção transversal de . é feita de alumínio e tem área de seção transversal de .
Dados: , , e .
Passo 1
O que está acontecendo?
A haste central de alumínio tem:
- Um comprimento inicial ;
- Um coeficiente de dilatação térmica ;
- Uma área de seção transversal ;
- Um módulo de elasticidade ,
& vai sofrer uma variação de temperatura .
Por outro lado, para as hastes laterais de aço e , vamos ter que:
- ;
- ;
- ;
- ;
- & .
Dessa forma, essas hastes vão sofrer dilatações térmicas que vão ser dadas pela fórmula:
Mas essas hastes não podem se dilatar livremente devido a existência da barra rígida que elas suportam.
Por causa dessa barra, as hastes têm que se dilatar de tal forma que:
- O deslocamento do ponto central da barra rígida (igual à variação de comprimento total da haste central de alumínio menos a folga )...
- ...seja igual ao deslocamento dos pontos laterais da barra rígida (igual à variação de comprimento total das hastes laterais de aço).
Ou seja:
Mas a variação de comprimento total de uma haste é a soma entre a dilatação térmica e a variação de comprimento causada pelo carregamento na haste.
Dessa forma, a expressão acima pode ser reescrita assim:
(Essa é a equação de compatibilidade desse sistema!)
E como vai ser o carregamento nas hastes?
Bom...
Como é quase o dobro de , podemos imaginar que a haste central de alumínio vai se dilatar muito mais que as hastes laterais e de aço.
Então vamos ter a haste empurrando a barra rígida para cima com uma força enquanto que e puxam a barra para baixo com forças e :
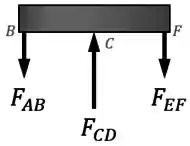
Como uma reação às forças e para baixo, a barra rígida vai puxar as hastes e para cima com forças de mesma intensidade, tracionando elas.
Já como uma reação à força para cima, a barra rígida vai empurrar a haste para baixo com uma força de mesmo intensidade, comprimindo ela.
São essas forças de tração e compressão que vão gerar as variações de comprimento e devido ao carregamento nas hastes, de acordo com a fórmula:
Onde é a força interna normal em cada haste.
E o que é que o exercício quer?
Ele quer que a gente encontre o valor das forças e .
Para encontrar essas forças, vamos ter que:
- Aplicar as condições de equilíbrio no diagrama de corpo livre da barra rígida que fizemos acima;
- & desenvolver a equação de compatibilidade que encontramos;
Com isso, vamos ter equações o suficiente relacionando os valores de , e para que a gente possa calcular essas forças! 💃
Passo 2
Então vamos começar fazendo o diagrama de corpo livre da barra ...
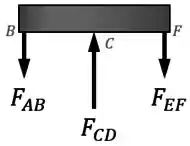
...e aplicando as condições de equilíbrio nessa barra!
Temos duas condições disponíveis aqui: o equilíbrio de forças na vertical e o equilíbrio de momentos em relação a um ponto.
Começando pelo equilíbrio de momentos em relação a um ponto, vamos escolher o ponto central :
Se a gente chamar de a distância entre o ponto central e as extremidades e , esse somatório de momentos fica assim:
O que significa que:
Já para o equilíbrio de forças na vertical, temos:
Fazendo esse somatório, encontramos que:
Isolando , temos:
Mas como acabamos de encontrar que , isso significa que:
Passo 3
Em seguida, vamos desenvolver nossa equação de compatibilidade.
Como vimos no Passo 1, temos que:
Nessa equação, podemos desenvolver as dilatações térmicas usando a fórmula:
Aplicando essa fórmula para a barra de alumínio e para as barras de aço, vamos ter que:
E podemos desenvolver as variações de comprimento devido ao carregamento nas peças usando a fórmula:
No nosso caso, temos que a força interna normal vai ser:
- E igual à para a haste central de alumínio que vai estar sob compressão.
- Igual à para as hastes laterais de aço que vão estar sob tração;
Então as variações para cada material vão ser:
Substituindo tuuuudo isso na nossa equação de compatibilidade, ela fica assim:
Eita!
Mas pensa aí... 🤔
Já temos o que precisamos para resolver o exercício:
- Queremos encontrar o valor da força ;
- E já temos duas equações (as equações 2 e 3) que relacionam as forças e , então podemos combinar essas equações para encontrar essas forças!
Passo 4
Então vamos substituir a equação 2 () na equação 3 que acabamos de encontrar no passo anterior.
Fazendo isso, vamos ter que:
Com isso, o nosso último objetivo é isolar nessa expressão!
Deixando todos os termos com de um lado e os demais termos do outro, essa expressão fica assim:
Colocando em evidência, temos que:
O que significa que:
Por fim, se substituirmos nessa expressão os seguintes valores...
- e ;
- e ;
- , e ;
- e ;
- & e ,
...e lembrarmos que é o mesmo que , vamos ter que todas as unidades vão estar em função de , e .
Então o resultado para a força nessa expressão vai sair em .
Substituindo tudo e calculando , que é igual à , vamos encontrar a nossa resposta: