Na coluna de concreto reforçada com vigas de aço abaixo, tanto o concreto quanto o aço estão fixados entre o solo e uma placa rígida.
A coluna possui um comprimento inicial . Além disso, o concreto e o aço possuem módulos de elasticidade e e áreas de seção transversal e .
Considerando que não existe nenhuma carga externa na coluna e que os materiais possuem coeficientes de dilatação térmica distintos , determine a força que a placa rígida fixa faz no concreto quando a coluna for submetida a uma variação de temperatura , fazendo o concreto e o aço sofrerem dilatações térmicas distintas e .
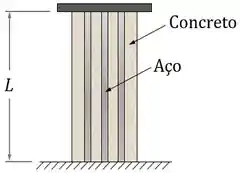
Dica do Expert: A placa rígida que fixa as extremidades do concreto e do aço vai forçar com que as variações de comprimento total dos dois materiais sejam iguais.
Passo 1
O que está acontecendo?
Se não fosse pela placa rígida, se o concreto e o aço estivessem livres um do outro, cada um sofreria as suas dilatações térmicas livremente:
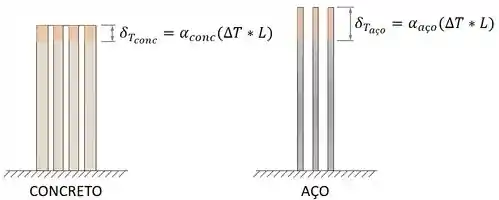
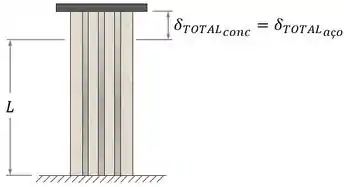
Mas, por causa da placa rígida, os materiais são forçados a ter a mesma variação de comprimento total:
Para que isso seja possível, o que acontece é que a placa rígida fixa exerce forças no concreto e no aço, e .
Esse carregamento gera forças internas normais e nos materiais, que, por sua vez, geram neles variações de comprimento e dadas pela fórmula:
Daí que essas variações de comprimento e devido ao carregamento nas peças se encarregam de compensar a diferença entre as dilatações térmicas e .
E o que é que o exercício quer?
Ele quer saber o valor da força que a placa rígida faz no concreto.
Para encontrar essa força, provavelmente vamos precisar tanto de uma equação de equilíbrio quanto de uma equação de compatibilidade.
Passo 2
A primeira coisa que podemos fazer para encontrar uma força é fazer o diagrama de corpo livre das pelas e aplicar as condições de equilíbrio nessas peças.
Fazendo esse diagrama de corpo livre para as nossas peças, ele fica assim:
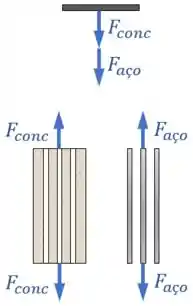
Como não sabemos ainda as direções das forças e , desenhamos ela com uma direção qualquer.
Aplicando o equilíbrio de forças na vertical para a placa rígida, temos que:
O que significa que:
Infelizmente, além disso, não tem mais nada que conseguimos extrair das equações de equilíbrio.
Então uma solução agora é encontrar uma equação de compatibilidade que nos permita relacionar as forças e de uma outra forma.
Passo 3
A verdade é que lá no Passo 1 a gente já viu uma equação de compatibilidade.
Vimos lá que, por causa da placa rígida, as variações de comprimento totais do concreto e do aço devem ser iguais:
Mas para usar essa equação de compatibilidade, precisamos desenvolver ela.
Primeiro, podemos pensar em como a variação de comprimento total em uma peça é a superposição das variações de comprimento devido à cada efeito que existe naquela peça.
No nosso caso, temos:
- Os efeitos térmicos, que geram uma dilatação térmica ;
- E os efeitos mecânicos (devido às forças na peça), que geram uma variação de comprimento .
Então a nossa equação de compatibilidade pode ser reescrita assim:
Se aplicarmos as fórmulas de e para o concreto e para o aço, isso fica assim:
Aqui, podemos observar duas coisas:
- Primeiro que como desenhamos no passo anterior as forças e como forças de tração, as forças internas normais vão ser e ;
- E segundo que podemos cortar em todos os termos dessa expressão acima.
Dessa forma, a expressão fica assim:
E pronto! Agora já temos duas equações diferentes relacionando e , o que é o suficiente para que a gente possa calcular essas forças.
Passo 4
Para encontrar , podemos substituir da equação 1 na equação 2.
Fazendo isso, temos que:
Colocando todos os termos com à esquerda e os demais à direita, temos:
Colocando e em evidência:
Daí que, finalmente, isolando , encontramos nossa resposta: