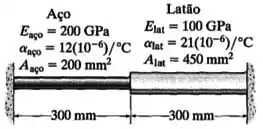
Duas barras feitas de materiais diferentes são acopladas e instaladas entre duas paredes quando a temperatura é . Determine a força exercida nos apoios (rígidos) quando a temperatura for . As propriedades dos materiais e as áreas de seção transversal de cada barra são dadas na figura.
Passo 1
O que está acontecendo?
Quando as barras de aço e de latão foram instaladas a uma temperatura inicial , elas não estavam nem sob compressão nem sob tração.
Além disso, elas têm:
- Comprimentos iniciais ;
- Módulos de Elasticidade e ;
- Coeficientes de Dilatação Térmica e ;
- E áreas de seção transversal e .
Quando a temperatura é elevada para , as barras sofrem uma variação de temperatura .
Por causa dessa variação de temperatura, cada barra sofre uma dilatação térmica :
Mas as barras estão restringidas entre duas paredes fixas, que não podem ser afastadas ou aproximadas.
Então a variação de comprimento total das duas barras deve ser nula:
Para garantir que isso ocorra, o que as paredes fazem é aplicar forças de reação nas barras, comprimindo-as de forma a anular as dilatações térmicas :
![]()
Essas forças de compressão geram uma força interna normal e uma variação de comprimento em cada barra.
E o que é que o exercício quer?
Ele quer que a gente descubra o valor da força que as barras aplicam nas paredes.
Pelo princípio da ação e reação, essa força vai ser igual à força que as paredes aplicam nas barras.
(Ou seja, o exercício quer descobrir o valor de !)
Para encontrar , vamos ter que desenvolver a equação de compatibilidade...
...até que ela seja descrita em função de .
Passo 2
Para desenvolver a equação de compatibilidade , podemos começar aplicando o princípio da superposição.
Com ele, podemos descrever essa variação de comprimento total das duas barras como a soma:
- Das variações individuais e causadas pela variação de temperatura em cada barra;
- Com as variações individuais e causadas pelas forças atuantes nas barras.
Dessa forma, temos que:
Vamos guardar essa equação.
Passo 3
Agora, podemos usar a fórmula da dilatação térmica para definirmos e :
E podemos usar a fórmula da variação de comprimento devido ao carregamento em uma peça para definirmos e :
E ainda vimos no Passo 1 que a força interna normal nas barras é igual à , de tal forma que:
Daí que substituindo essas fórmulas naquela expressão que tínhamos guardado ao final do passo anterior, ela fica assim:
Dividindo tudo por , conseguimos simplificar essa expressão:
Assim, conseguimos fazer o que queríamos que era desenvolver a equação de compatibilidade até que ela fosse descrita em função da força desconhecida.
Com isso, só nos falta isolar para encontrarmos o seu valor.
Passo 4
Para isolar na expressão anterior, começamos colocando e em evidência:
Passamos o termo com para o outro lado:
E finalmente isolamos encontrando que:
Se substituirmos:
- ;
- e ;
- e ;
- & e ,
Todos os valores vão estão em função das unidades , e . Então o nosso resultado para a força vai sair em .
Fazendo essas substituições e calculando tudo, encontramos nossa resposta: