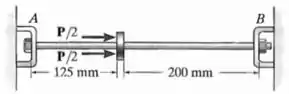
A haste de alumínio 2014-T6 tem diâmetro de e está levemente conectada aos apoios rígidos em e quando . Se a temperatura baixar para e uma força axial for aplicada ao colar rígido, como mostra a figura, determine as reações em e .
Dados: , .
Passo 1
O que sabemos sobre a haste?
A haste tem um comprimento inicial .
Ela é dividida pelo colar rígido (que podemos chamar de “”) em dois segmentos de comprimentos iniciais e .
Além disso, ela tem um diâmetro , módulo de elasticidade , coeficiente de dilatação térmica e uma temperatura inicial .
E ela está levemente conectada aos apoios rígidos em e , ou seja, os apoios não realizam nenhuma força significativa na haste.
E o que é que está acontecendo?
Quando a temperatura é abaixada para , a haste sofre uma variação de temperatura .
Por causa dessa variação de temperatura, ela sofre uma contração térmica :
Mas os em e em são fixos.
Então eles vão aplicar na haste reações e com as intensidades que forem necessárias para que a variação de comprimento total na haste seja nula:
E, em seguida, ainda é aplicado na haste a carga axial no ponto .
Dessa forma, o diagrama de corpo livre da haste fica assim:
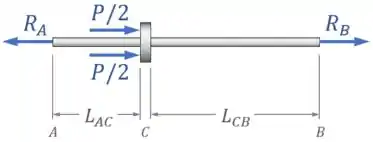
Essas cargas vão gerar nos segmentos e forças internas normais e .
Essas forças normais, por sua vez, vão gerar variações de comprimento nos segmentos e .
Daí que pelo princípio da superposição, vamos ter que a variação de comprimento total na haste vai ser a soma:
- Da dilatação térmica ;
- Da variação de comprimento do segmento , ;
- E da variação de comprimento do segmento , ;
Ou seja:
E o que é que o exercício quer?
Ele quer saber qual vai ser o valor das reações e .
Para encontrar o valor dessas reações, podemos aplicar uma equação de equilíbrio na haste para relacionar as reações com a força .
Mas isso não vai ser o suficiente para encontrar as duas incógnitas e .
Então também vamos ter que desenvolver a equação de compatibilidade para podermos relacionar e de alguma outra forma.
Passo 2
Então vamos começar fazendo o diagrama de corpo livre da haste para, em seguida, aplicarmos as condições de equilíbrio nela:
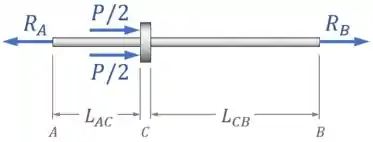
Aqui, a única condição que temos disponível é o somatório de forças na horizontal:
Fazendo esse somatório, vamos ter que:
O que significa que:
Infelizmente, essa relação não é suficiente para que a gente possa encontrar e .
Então vamos guardar ela por enquanto e seguir para o próximo passo, que é desenvolver a nossa equação de compatibilidade.
Passo 3
Para desenvolvermos os termos e da equação de compatibilidade, temos que conhecer:
- Os valores das forças normais nos segmentos e ;
- E o valor da área da seção transversal da haste.
Para encontrar o valor das forças , vamos fazer uma análise dos esforços internos na haste:
Para seções entre e , essa análise fica assim:

Pelo equilíbrio de forças, temos que:
E para as seções entre e , fica assim:

E o equilíbrio de forças nos mostra que:
Já quanto a área da seção transversal da haste, sabemos que ela é uma área circular de diâmetro .
Então podemos aplicar a fórmula da área do círculo em função de seu diâmetro:
E substituir para encontrarmos que:
Passo 4
Agora sim podemos desenvolver a nossa equação de compatibilidade:
Nessa equação, podemos desenvolver a dilatação térmica usando a sua fórmula, que vai ficas assim para a nossa haste de alumínio:
E podemos desenvolver as variações de comprimento e devido aos carregamentos em cada segmento da haste usando a fórmula .
Aplicando essa fórmula para cada um dos dois segmentos, temos:
E como e , ainda podemos dizer que:
Dessa forma, a nossa equação de compatibilidade pode ser reescrita assim:
E pronto!
Agora podemos combinar as Equações 1 e 2 para encontrarmos os valores de e !
Passo 5
Substituindo a Equação 1 () na Equação 2, temos que:
Aqui, se conseguirmos isolar nessa equação, vamos conseguir encontrar o seu valor.
Para isolar , podemos primeiro passar para o outro lado e colocar em evidência:
Em seguida, passamos para o outro lado e desenvolvemos o lado esquerdo:
E depois, passamos para o outro lado e colocamos em evidência:
Por fim, conseguimos isolar e encontrar que:
Se quisermos, ainda podemos perceber que a soma dos comprimentos dos dois segmentos da haste é o mesmo que o comprimento total da haste.
Dessa forma, a expressão para fica assim:
E ainda pode ser simplificada para ficar assim:
Substituindo os valores...
- ;
- ;
- & ,
...vamos encontrar que o termo vale:
Já substituindo...
- ;
- ;
- & ,
...vamos encontrar que vale:
Sendo assim, vai ser:
Encontrado , podemos voltar na Equação 1:
E substituir e para encontramos que:
E assim terminamos o exercício! 🎉