Um fabricante de relógios deseja conhecer a variabilidade do seu produto. Para isso registrou os desvios de relógios em segundos relativos a um relógio de alta precisão, ocorridos ao fim de um mês e obteve como resultado: média de segundos e desvio padrão de segundos.

Pede-se

a) Com base na longa experiência com os relógios desta marca, o fabricante acredita que o verdadeiro desvio padrão é no máximo segundos. Ao nível de significância de , podemos afirmar que o fabricante está correto?

b) Determine se o fabricante pode afirmar que a verdadeira média é igual a segundo ao nível de significância de .

Bom, nós já definimos as hipóteses no item (a). Agora temos que lembrar que o nível de significância corresponde a probabilidade de um erro do tipo , que denotamos pela letra . Nesse caso, temos

Esse número corresponde à probabilidade de rejeitarmos a hipótese quando ela é verdadeira.

Nesse caso, temos um teste unilateral à esquerda, pois a limitação da hipótese alternativa é . Por uma questão de notação, vou escrever . Desta forma, temos

Além disso, como queremos analisar a distribuição da variância, temos que lembrar que

A variável segue uma distribuição do tipo qui-quadrado. Você lembrar que é a variância amostral:

Já é a variância real. Nesse problema temos uma amostra com , de modo que

A seguir faço um esboço da distribuição de qui-quadrado:

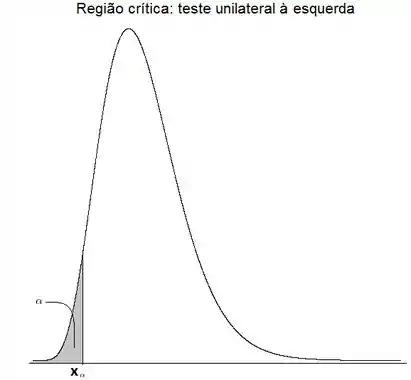
Como o teste é unilateral à esquerda, a região crítica será determinada como a região pintada na figura, em que a probabilidade deve ser . Vamos determinar que delimita essa região!

A variável segue uma distribuição do tipo , de modo que vamos precisar olhar na tabela da distribuição de qui-quadrado fornecida na prova. No cabeçalho da tabela temos:

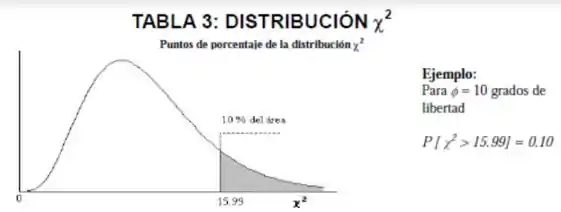
Importante notar que os dados da tabela são do tipo . Com isso, temos que

Daí, olhamos na tabela para a linha com graus de liberdade e na coluna com probabilidade . Fazendo isso, achamos:

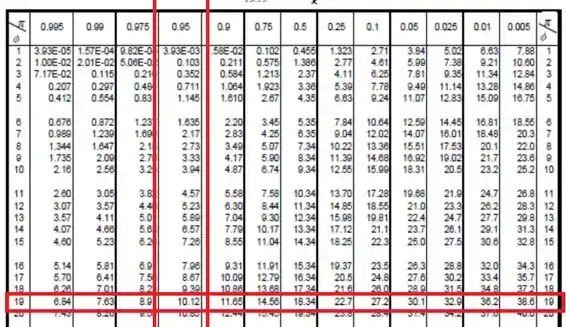
Agora, usando o valor referência , nós calculamos :

A condição para rejeitarmos a hipótese nula no caso unilateral à esquerda é

Mas nesse caso isso não acontece pois claramente temos que é maior que . Portanto, a hipótese nula não pode ser rejeitada e o fabricante está errado!

No item (a) vimos que o fabricante estava errado em dizer que o desvio padrão máximo era de segundos dentro de um nível de significância de . Agora vamos ao item (b), em que devemos descobrir se o fabricante pode dizer que a média é dentro do nível de significância de .

Desta vez, nossas hipóteses serão:

Trata-se de um típico teste bilateral. Além disso, como esse teste é sobre a média, vamos usar a distribuição de Student para a variável

Nesse problema, e , de modo que

Ou ainda,

Agora vamos olhar para a distribuição de Student no caso bilateral:

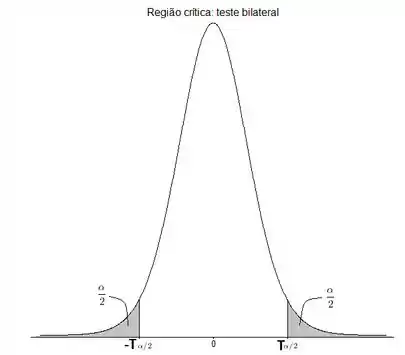
Como o teste é bilateral, a probabilidade de estar fora da faixa central será dividida em duas metades, uma para cada lado. Temos, portanto,

No cabeçalho da tabela da distribuição de Student, temos

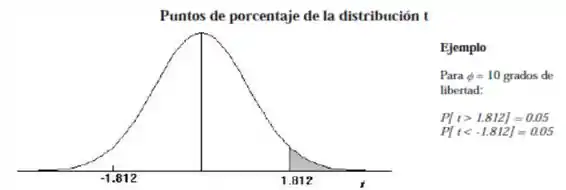
Vemos que o que é fornecido na tabela é exatamente o que nós queremos achar (). Indo na linha dos graus de liberdade e na coluna , achamos

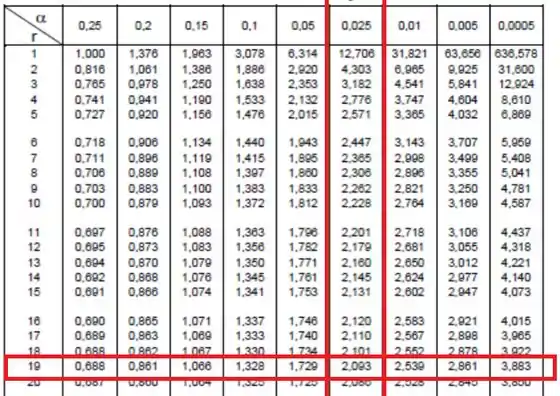
Portanto,

O critério do teste é que devemos aceitar se

Para calcular usamos :

A condição do teste é satisfeita, de modo que a hipótese deve ser aceita. Como essa hipótese é que a média seja , o fabricante pode afirmar, dentro da significância de , que a média é .

Com isso nós terminamos o problema 😊.