Um fabricante de relógios deseja conhecer a variabilidade do seu produto. Para isso registrou os desvios em segundos de 24 relógios, relativamente a um relógio de alta precisão ocorridos ao fim de um mês e obteve como resultado: média de 0,8 segundos e desvio padrão de 1,5 segundo.
Pede-se:
- Com base na longa experiência com os relógios desta marca o fabricante acredita que o verdadeiro desvio padrão é no máximo 1,2 segundos. Ao nível de significância de 1% e 5% podemos afirmar que o fabricante está correto?
Mostre claramente o seu desenvolvimento para o teste de hipótese determinando: as hipóteses nula e alternativa, a estatística do teste e a decisão acompanhada de um gráfico da função de probabilidade da estatística do teste, indicando claramente as áreas de rejeição e de aceitação de .
Passo 1
a)
As informações da nossa amostra são:
E nossa amostra tem 24 relógios, então:
Passo 2
Queremos testar o desvio padrão ser no máximo 1,2 segundos, então:
Sinal de igualdade sempre! Como é no máximo 1,2 segundos, qualquer valor menor que 1,2 segundos ainda conta. Então nossa alternativa tem que ser o contrário disso, ou seja, tem que ser maior que 1,2 segundos:
Passo 3
Teste de hipótese para desvio padrão a gente vai usar a distribuição qui-quadrado!
Vamos começar pelo nível de significância de 1%, ou seja:
Na curva da qui-quadrado, teríamos isso aqui:
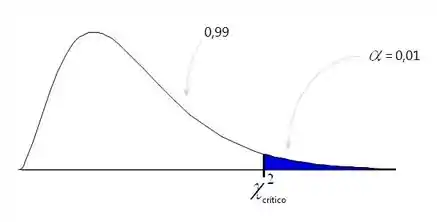
na ponta direita porque nossa hipótese alternativa tem o sinal de maior que! E como a área abaixo da curva tem que ser 1, achamos a área em branco fazendo .
Lembrando que a região de rejeição está em azul e a de aceitação está em branco!
Passo 4
Nosso vai ser então:
Já que temos à direita da curva, separando a região crítica da região de aceitação.
E como temos uma amostra de 24, nosso grau de liberdade será:
Procurando esse qui-quadrado na tabela, temos:
Passo 5
A nossa estatística de teste vai ser:
Substituindo os valores que temos (lembrando que a variância é o valor que estamos testando):
Passo 6
Agora temos que ver se ela tá na área azul ou branca do gráfico:
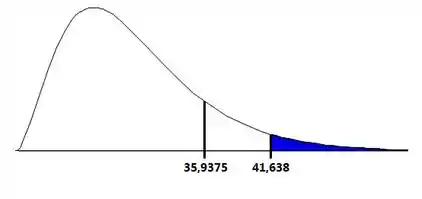
Branca! Então não rejeitamos a hipótese nula.
Passo 7
Mas não acabou por aí hehe
Agora, vamos fazer tudo novamente, só que com o nível de significância de 5% e mantendo o mesmo grau de liberadade. Com isso,
Olhando na tabela, teremos:
Agora, vamos avaliar em qual região se encontra a nossa estatística de teste, .
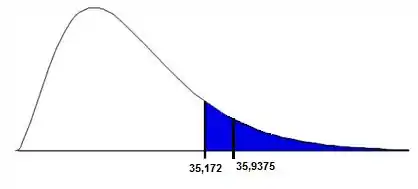
E como estamos na região azul, para um nível de significância de 5%, deveremos rejeitar a hipótese nula.