TAREFA da aula – 10 – Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 4
A performance nominal de uma ferramenta de corte é em média de 970 peças cortadas por vida útil com desvio padrão de 7 peças. Uma amostra de 5 destas ferramentas apresentaram performance em suas vidas úteis de: média = 1003 e variância = 145. Podemos dizer, para o nível de 5% de significância, que a média e a variância da performance nominal desta ferramenta aumentaram? Teste as hipóteses.
Defina claramente suas hipóteses. Mostre o resultado através do cálculo da estatística do teste. Esboce um gráfico da distribuição do teste indicando claramente a área de rejeição e aceitação de .
Passo 1
Última questão da última lista, galerinha! Que belezinha!?
Bom! Nesse exercício aqui, queremos testar se a média e a variância da vida útil das peças aumentaram ou continuam as mesmas.
Começando pela média, nossas hipóteses serão:
Temos nosso desvio padrão populacional, então vamos fazer um teste de hipóteses unilateral superior clássico!
Passo 2
Começando calculando a estatística de teste:
Passo 3
Agora vamos calcular nosso . Lembrando que :
Procurando na tabela da Normal abaixo...
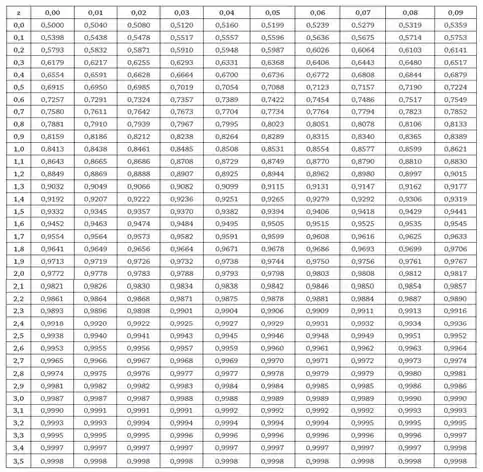
Temos que:
Passo 4
Então, nosso gráfico fica:
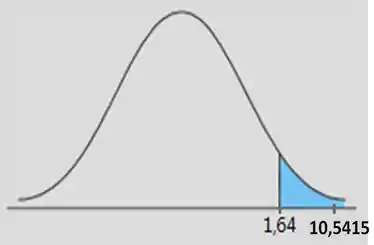
Então nossa estatística de teste tá dentro da região crítica, ou seja, rejeitamos ! Temos evidências para dizer que a média dos desvios aumentou.
Passo 5
E agora vamos testar a variância. Montando as hipóteses, obtemos que:
Temos então um teste de hipóteses para variância unilateral superior!
Passo 6
Calculamos primeiro, nossa estatística de teste:
Substituindo os valores:
Passo 7
Agora vamos determinar nosso , que no unilateral superior é dado por:
Como :
E lembrando que vamos ter grau de liberdade , procuramos esse qui-quadrado na tabela, temos que:
Passo 8
Nosso gráfico fica então:
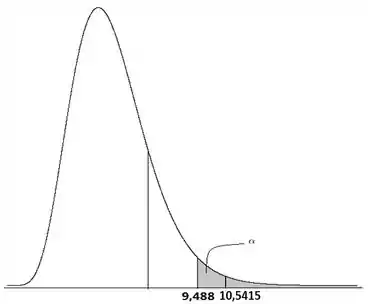
E a estatística de teste caiu dentro da região crítica, então novamente rejeitamos ! Ou seja, podemos afirmar que a variância dos desvios aumentou.