Pesquisadores de uma clínica de emagrecimento desejam comparar a eficácia de uma dieta com exercícios contra uma dieta sem exercícios. Setenta e dois pacientes foram aleatoriamente selecionados e divididos em dois grupos. O primeiro grupo, com pacientes, foi colocado no programa de dieta com exercícios. O segundo grupo, com pacientes, foi colocado no programa de dieta sem exercícios. Os resultados com a perda de peso, em quilogramas, após 4 meses foram:
Grupo 1: média amostral de e desvio padrão amostral de .
Grupo 2: média amostral de e desvio padrão amostral de .
Pede-se:
a) Através do teste de hipótese para a média, determine com o nível de significância de se existe diferença entre as médias do tratamento do grupo 1 () para o tratamento do grupo 2 ().
b) Através do teste de hipótese para a variância, determine com o nível de significância de se existe diferença entre as variâncias do tratamento do grupo 1 () para o tratamento do grupo 2 ().
Passo 1
Antes de qualquer coisa, vamos calcular o desvio padrão da média de cada grupo:
Para o grupo 1:
Já para o grupo 2:
Esses serão os desvios padrão que usaremos nos testes de hipótese, por isso a primeira coisa que eu fiz foi calculá-los!
Passo 2
No item (a) queremos fazer um teste de hipótese para comparação das médias. O primeiro passo para isso é determinar as hipóteses. Queremos saber se as médias são iguais ou não e, para isso, nossas hipóteses devem ser:
Trata-se de um teste bilateral! Se a hipótese for descartada, concluímos estatisticamente que as médias são diferentes.
Passo 3
Para fazer esse teste de comparação entre as médias, faremos um teste T de Student com a a variável:
Essa variável segue uma distribuição de Student com graus de liberdade, onde
Substituindo os valores:
Como precisamos de um valor inteiro, vou arredondar para
Aqui vai uma observação bem importante que muita gente não sabe: quando o número de graus de liberdade é grande (tipicamente bem acima de 30), podemos aproximar a distribuição de Student por uma distribuição normal. É isso que vamos fazer nesse problema!
Passo 4
Como o número de graus de liberdade é bem elevado, podemos dizer que a variável segue uma distribuição normal com média e desvio padrão assim como a tradicional variável que usamos para esses problemas. Portanto, o esboço da região proibida pelo teste bilateral é dado a seguir:
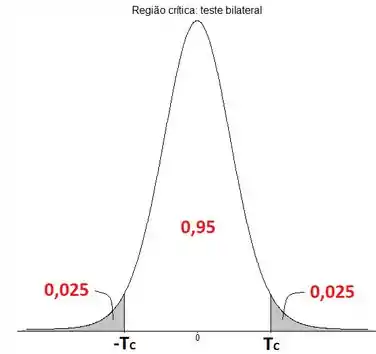
Queremos achar o valor de tal que
Daí, é só olhar na tabela da distribuição normal:
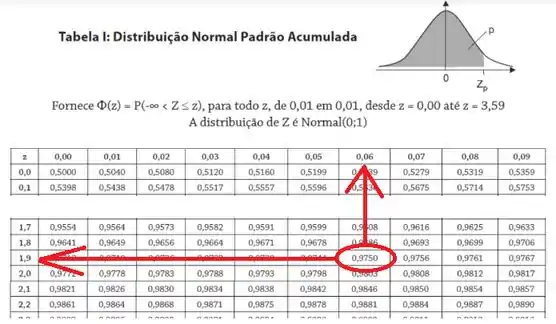
Vemos que
Passo 5
Agora você precisa lembrar que no teste bilateral, nós rejeitamos se
Isso significa que
Como estamos testando a hipótese , temos que
Fazendo as contas: e . Portanto, para que seja rejeitada, devemos ter:
Se for rejeitada, podemos afirmar que a médias são diferentes dentro da significância considerada. Mas note que
Vemos claramente que a condição para rejeição de não é satisfeita. Portanto, não podemos afirmar estatisticamente que as médias são diferentes.
Passo 6
Agora vamos olhar para o item (b)! Devemos fazer a mesma coisa que fizemos no item (a), mas agora o teste será sobre a variância!
As hipóteses são:
Trata-se novamente de um teste bilateral! A grande diferença desse item para o que fizemos no item (a) é que para a variância não fazemos o teste T, e sim o teste F usando a distribuição de Snedecor!
Introduzimos a variável:
Lembrando que e são os desvios padrão amostrais. Essa variável deve seguir uma distribuição de Snedecor com e graus de liberdade.
Passo 7
Por se tratar de um teste bilateral, o esboço da região crítica é:
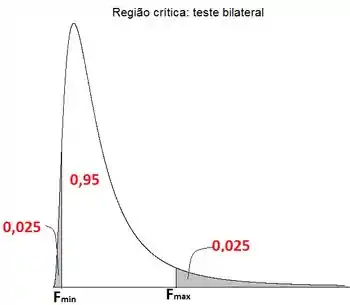
Para achar o , devemos ter
Aí vamos para a tabela:
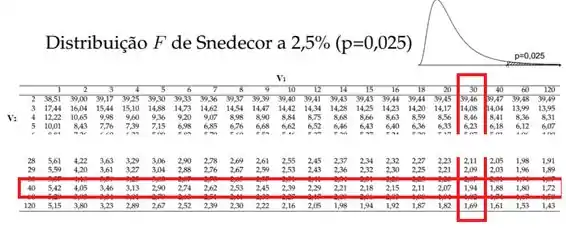
Achamos que
Agora temos que achar , mas antes de fazer isso vou fazer uma consideração...
Para que a hipótese seja considerada, devemos ter
Portanto, se , a hipótese não pode ser descartada e não podemos afirmar estatisticamente que a variâncias são distintas.
Pela figura da distribuição, é fácil perceber que deve ser um número bem pequeno. Usando e , temos que
Com certeza será menor que . Portanto, a condição para que seja rejeitada não é satisfeita, de modo que não podemos afirmar estatisticamente que as variâncias são diferentes.
PS: eu fiz essa análise qualitativa para o pois a prova não fornecia a tabela dessa situação.
Resposta
a) Não podemos afirmar estatisticamente que as médias são diferentes.
b) Não podemos afirmar estatisticamente que as variâncias são diferentes.