Três dados são lançados e os valores obtidos, a, b e c, compõem a matriz . Qual é a probabilidade de A não ser invertível? (Os dados têm seis faces numeradas de 1 a 6, todas com a mesma probabilidade de ocorrência).
(a) 2 chances em 216
(b) 12 chances em 216
(c) 15 chances em 216
(d) 25 chances em 216.
Passo 1
O enunciado quer que a gente analise as possíveis combinações de a, b e c para que a matriz A não seja invertível.
É equivalente dizer:
- A é não invertível
- A possui colunas ou linhas LD
Nesse caso, vai ser mais fácil forçarmos uma condição para que as linhas de A sejam LD.
Vamos começar escalonando a matriz.
Passo 2
Escalonando:
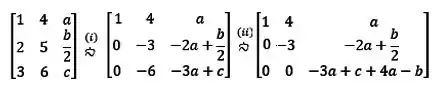
Passo (i): e
Passo (ii):
Para que as linhas sejam LD, a última teria que ser toda igual a zero. Logo:
Passo 3
Então, para valores de a, b e c que satisfaçam a relação acima, as linhas serão LD e a matriz não será invertível.
Como os valores de a, b e c vêm de um dado, eles estão restritos a números de 1 a 6.
Então, vamos montar uma tabela, vendo os valores possíveis para cada uma dessas incógnitas que satisfaçam a relação.
Vamos ficar com algo mais ou menos assim:
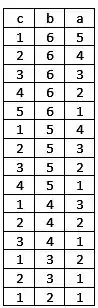
Temos então 15 combinações possíveis para a, b e c que satisfazem a relação que achamos antes.
No total, temos combinações possíveis para a, b e c (6 valores para a, 6 para b e 6 para c).
Portanto, a probabilidade de a matriz A não ser invertível é de 15 em 216.
Passo 4
Resposta
(c) 15 chances em 216