Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Valor Médio de uma Função

Ver Teoria
Exercício 61234578910111213

Enunciado

UFABC; Funções de Uma Variável; Listas FUV - GRADMAT; Lista 10 - Técnicas de Integração II ; Questão 9

Ache o centróide de massa da região R abaixo da curva   y   = 2 x x 2   + 1 no intervalo [ 0 ,   2 ] .

Passo 1

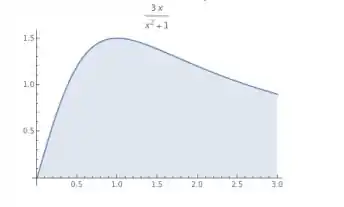
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1. Essa questão tem como objetivo encontrar o centróide (centro de massa) da região R abaixo da curva   y   = 2 x x 2   + 1 no intervalo [ 0 ,   2 ] .

Eita, mas qual é a definição de centróide de uma região mesmo?

Vamos revisar, pois é um conceito simples, porém um pouco delicado

Vamos nessa!!!

Passo 2

O Centróide de uma região definida por uma função e o eixo x é o ponto ( x ̄ , y ̄ ) onde:

x ̄   =   ∫ R x d A   / ∫ R d A  

com

d A   =   y d x

e

y ̄   =   ∫ R y 2 d A   / ∫ R d A  

Vamos analisar cada parte dessas equações com calma.

O que seria ∫ R d A ? Bem Isso é a área da nossa região, ou seja, a área abaixo da curva   y   = 2 x x 2   + 1 no domínio de interesse, que é [ 0,2 ] na nossa questão.

Então o nosso ponto ( x ̄ , y ) ̄ seria uma “média” ponderada pela área da região, o que faz sentido para uma definição de centróide (centro de massa com densidade constante em toda região)

Agora que revisamos as fórmulas, vamos aplicar.

Passo 3

Agora que relembramos a fórmula, vamos aplicar!!! Vamos obter a área da nossa região:

A   = ∫ R y d x  

= ∫ 0 2 2 x x 2 + 1 d x

fazendo u   =   x 2   ⇒   d u   =   2 x d x , Logo:

∫ 2 x x 2 + 1 d x = ∫ d u u + 1

= l n ( u + 1 )

retornando para a variável original e calculando os limites de integração, temos:

∫ 0 2 2 x x 2 + 1 d x   =   l n ( 5 )

Prontinho, a área da nossa região é   l n ( 5 ) . Agora vamos calcular o centróide

Passo 4

Vamos calcular x ̄ . Como vimos no passo 1, temos:

x ̄   =   ∫ R x d A   / ∫ R d A  

=   ∫ R x y d x   / ∫ R y d x  

Sabemos quem é y é a nossa função, então

=   ∫ 0 2 x ( 2 x x 2 + 1 ) d x   / l n ( 5 )  

=   ∫ 0 2 2 x 2 x 2 + 1 d x   / l n ( 5 )  

fazendo a divisão polinomial

=   ∫ 0 2 2 - 2 x 2 + 1 d x   / l n ( 5 )  

mas essas integrais já são manjadas!!!!

=   [ 2 x - 2 t g - 1 ( x ) ]   / l n ( 5 )   | x = 0 x = 2

Resolvendo temos que

x ̄   =   ( 4   -   2 t g - 1 ( 2 ) ) / l n ( 5 )

Passo 5

Agora precisamos calcular y ̄ . Vamos lembrar que no nosso problema

y ̄   =   ∫ R y 2 d A   / ∫ R d A  

como y   =   2 x x 2   + 1

então

  ∫ R y 2 d A   / ∫ R d A   =   ∫ 0 2 2 x 2 ( x 2 + 1 ) 2 d x   / l n ( 5 )

Vish, que integral feia!!!

Mas vamos com calma. Vamos separar esse denominador, então

  ∫ 0 2 2 x 2 ( x 2 + 1 ) 2 d x   / l n ( 5 ) =     ∫ 0 2 1 ( x 2 + 1 ) - 1 ( x 2 + 1 ) 2 d x   / l n ( 5 )

Opaaa, uma delas sabemos resolver. Vamos tentar resolver a outra!!!

Passo 6

Vamos resolver ∫ 1 ( x 2 + 1 ) 2 d x . Fazendo x   =   t g ( u )   ⇒ d x   =   s e c 2 ( u )

∫ 1 ( x 2 + 1 ) 2 d x = ∫ s e c 2 u * 1 ( t g ( u ) 2   +   1 ) 2 d u

mas t g 2 ( u )   +   1   =   s e c 2 ( u ) então

∫ s e c 2 ( u ) * 1 ( t g ( u ) 2   +   1 ) 2 d u = ∫ 1 s e c 2 ( u ) d u

simplificando tudo

= ∫ c o s 2 ( u ) d u

Mas essa integral já é manjada!!! Temos:

∫ c o s 2 ( u ) d u = 1 2 ( u   + s i n ( u ) c o s ( u ) )

retornando para a variável original x   =   t g ( u )   ⇒ u   =   t g - 1 ( x )

= 1 2 ( t g - 1 ( x )   + s i n ( t g - 1 ( x ) ) c o s ( t g - 1 ( x ) ) )

Então:

  ∫ 0 2 1 ( x 2 + 1 ) - 1 ( x 2 + 1 ) 2 d x   / l n ( 5 ) =   ( t g - 1 ( x ) - 1 2 ( t g - 1 ( x )   - s i n ( t g - 1 ( x ) ) c o s ( t g - 1 ( x ) ) ) ) / l n ( 5 ) | x = 0 x = 2

Para finalizar, vamos calcular os limites de integração

Passo 7

  ∫ 0 2 1 ( x 2 + 1 ) - 1 ( x 2 + 1 ) 2 d x   / l n ( 5 ) =   ( t g - 1 ( x ) - 1 2 ( t g - 1 ( x )   - s i n ( t g - 1 ( x ) ) c o s ( t g - 1 ( x ) ) ) ) / l n ( 5 ) | x = 0 x = 2

=   ( 1 2 ( t g - 1 ( 2 )   - s i n ( t g - 1 ( 2 ) ) c o s ( t g - 1 ( 2 ) ) ) ) / l n ( 5 )

Então nosso ( x ̄ , y ̄ ) ponto do centróide é:

y ̄ =   ( 1 2 ( t g - 1 ( 2 )   - s i n ( t g - 1 ( 2 ) ) c o s ( t g - 1 ( 2 ) ) ) ) / l n ( 5 )

x ̄   =   ( 4   -   2 t g - 1 ( 2 ) ) / l n ( 5 )

Prontinho, pessoal. Finalmente terminamos mais uma questão!!! Nessa questão revisamos a definição de centróide de uma região e como calcular. Deu para ver que dependendo da região os cálculos ficam bem extensos. Mas não desanimem, pois é uma oportunidade de treinar as nossas técnicas de integração .Espero que os passos tenham ficado claros. Até a próxima questão!!!

Resposta

x ̄   =   ( 4   -   2 t g - 1 ( 2 ) ) / l n ( 5 )

y ̄ =   ( 1 2 ( t g - 1 ( 2 )   - s i n ( t g - 1 ( 2 ) ) c o s ( t g - 1 ( 2 ) ) ) ) / l n ( 5 )

Exercícios de Livros Relacionados

Use o diagrama para mostrar que se f é côncava para cima em [ a , b ] , então f m e df a - b 2
Encontrar a massa total e o centro de massa de uma barra de 5 m de comprimento, sabendo que a densidade linear num ponto é uma função do 1º grau da distância total desse ponto ao extremo direito da ba
(a) Encontre o valor médio de f no intervalo dado.(b) Encontre c tal que f m e d = f ( c ) .(c) Esboce o gráfico de f e um retângulo cuja área seja a mesma que a área sob o gráfico de f. f x = x - 3 2
Use o resultado do Exercicio 77 na seção 5.5 para calcular o volume médio de ar inalado pelos pulmões em um ciclo respiratório.
Ache o valor de χ que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema. ∫ 1 2 x 3 = 15 4