Seja definido no intervalo Seja c um ponto que satisfaz o Teorema do Valor Médio com respeito aos extremos do intervalo de definição. O valor de é:
Passo 1
Opa galera, aqui é uma questão de cálculo diferencial onde nós temos uma função qualquer que está definida e bem comportada ao longo de um certo domínio explicitado pela questão e a questão garante a existência de um ponto que satisfaz o teorema do valor médio. Para resolver o probleminha precisamos lembrar como se calcula uma derivada de um polinômio para utilizar isso em conjunto com o teorema do valor médio. Mas eis a pergunta, você se lembra do teorema do valor médio?

CAAAAAAAAAALMINHA, não precisa se preocupar vamos lembrar desse conceito bem importante aqui, o Teorema do valor médio ou o famoso TVM ele fala o seguinte:
Geometricamente a derivada é o coeficiente angular da reta tangente, o TVM nos informa que podemos calcular a derivada em um único ponto através da secante da curva, graficamente estamos fazendo a seguinte operação:
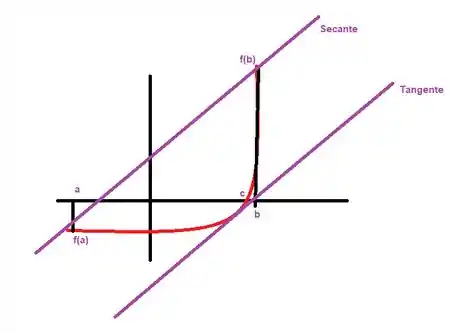
Iae conseguiu enxergar que a reta tangente é paralela a secante nesse caso? Então vamos utilizar o teorema do valor médio para calcular em qual ponto é possível realizar isso nesse caso.
Vamos lá?
Passo 2
Primeiramente vamos precisar da derivada da função, utilizando as propriedades das derivadas vamos calcular a derivada da .
Agora que calculamos a derivada precisamos calcular os parâmetros da secante, olhando a figurinha abaixo temos que precisamos de dois valores e também precisamos da .
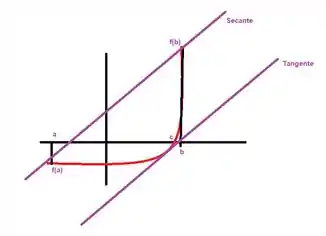
Utilizando a calculadora para simplificar as coisas temos os seguintes valores:
E agora temos todos os dados que precisamos para resolver o problema, sabe o que falta? Usar a formulinha do TVM. Rapidinho né?

Passo 3
Pela formulinha do TVM temos que
Utilizando os valores que já calculamos e usando temos que:
Resultando na seguinte equação:
Que consequentemente temos que:
Agora temos uma equação de segundo grau e para resolve-la precisamos utilizar a fórmula de Bhaskara.
Passo 4
Para finalizar, precisamos utilizar a formula de Bhaskara:
Gerando as seguintes soluções:
Tendo como resposta a alternativa que é
Resposta
A resposta é a alternativa e).