UFMG, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFMG - Lista 1 - Integrais Duplas e Triplas, Questão 17
Considere o sólido exterior ao cone e interior à esfera . Calcule, utilizando coordenadas esféricas, a massa total do sólido sabendo que a densidade de massa em cada ponto do sólido é proporcional à distância desse ponto à origem.
Passo 1
Eaew, belezinha?
Temos um sólido delimitado inferiormente pelo cone e superiormente pela esfera . Precisamos calcular a massa desse sólido, sabendo que a densidade em um ponto é proporcional a distância do ponto à origem. Mas, como calculamos a massa de um corpo usando integração? É bastante direto! Precisamos calcular a seguinte integral tripla
em que é a densidade de massa do sólido . Vamos precisar determinar um formato para esta densidade e obter os limites de integração que descrevem o nosso sólido! Bora lá!
Passo 2
Primeiro, vamos discutir um formato para a nossa densidade. Ele diz que para um ponto , temos que a densidade é proporcional a distância deste ponto à origem, a distância de um ponto qualquer à origem é dado como a norma do vetor
Usando a definição de norma, temos que
Portanto, a densidade pode ser definida como
em que é uma constante de proporcionalidade! Portanto, precisamos resolver a seguinte integral tripla
Beleza! Vamos analisar a nossa região agora!
Passo 3
A região delimitada é a seguinte
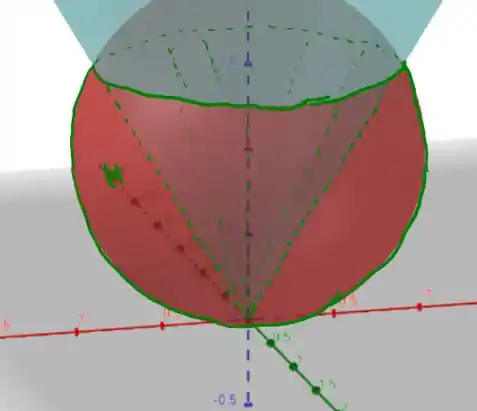
é como se cavasse um buraco na esfera com o formato do cone! Agora, o segredo é escolher um sistema de coordenadas que facilite a nossa vida, tendo em vista o formato da densidade e as simetrias de nosso problema, parece que o melhor caminho é usar coordenadas esféricas da forma
nestas coordenadas temos que o elemento de volume é dado por . E, portanto, a nossa integral se torna
em que se pode identificar que . Note também que o ângulo polar dá uma volta completa em nossa sólido, portanto o ângulo está no intervalo , no entanto ainda precisamos encontrar os limites para o ângulo e a coordenada radial! Bora lá!
Passo 4
Se aplicarmos as coordenadas esféricas na equação de nossa esfera obtemos que
portanto, temos que
de forma que temos a coordenada radial no intervalo . Agora, a equação do cone se torna
ou simplesmente
Isso nos dá o seguinte vínculo
que é verdadeiro para . Sendo assim, podemos garantir que o nosso intervalo para é , já que a figura só está no plano acima de . Maravilha! A integral que temos que resolver é então dada por
Vamos começar a integrar finalmente! Vem comigo!
Passo 5
Devemos integrar primeiro em , pois os seus limites são funções das outras variáveis, sendo assim, comecemos por
essa integral pode ser resolvida usando a regrinha
de forma que temos o resultado
Portanto, resta resolver
Vamos resolver a integral em agora! Saca só!
Passo 6
Temos que resolver a seguinte integral
para isso é conveniente utilizar uma substituição simples da forma
e
Portanto, a integral se torna
os limites são
e
e, portanto, a integral se torna
usando a mesma regrinha que utilizamos na integral da coordenada radial, temos que
Portanto, o nosso resultado é
e, nos resta resolver
Uff… quase acabando! Bora Bora!
Passo 7
Resolvendo a integral em , temos que
temos então que
Vamos tentar reescrever isso para identificar a resposta dada pelo problema, temos que
como temos que , podemos escrever que
Aí está! A questão foi isso! Te vejo na próxima! Tchau Tchau!